Harmonic Drive RSF supermini Series - Calculation Formulas for Mass and Moment of Inertia

A-2 Moment of inertia
A-3
10
11
付
付
4
5
App
Appendix
6-2 Moment of inertia
1. Calculation formulas for mass and moment of inertia
(1) When center of revolution and line of center of gravity match
Calculation formulas for mass and moment of inertia are shown below.
m:Mass (kg), Ix, Iy, Iz: moment of inertia (kgm
2
) making Axes x, y and z as centers of revolution
G：Distance from edge surface of center of gravity (m)
ρ：Density (kg/m
3
)
Units - Length: m, mass: kg, moment of inertia: kgm
2
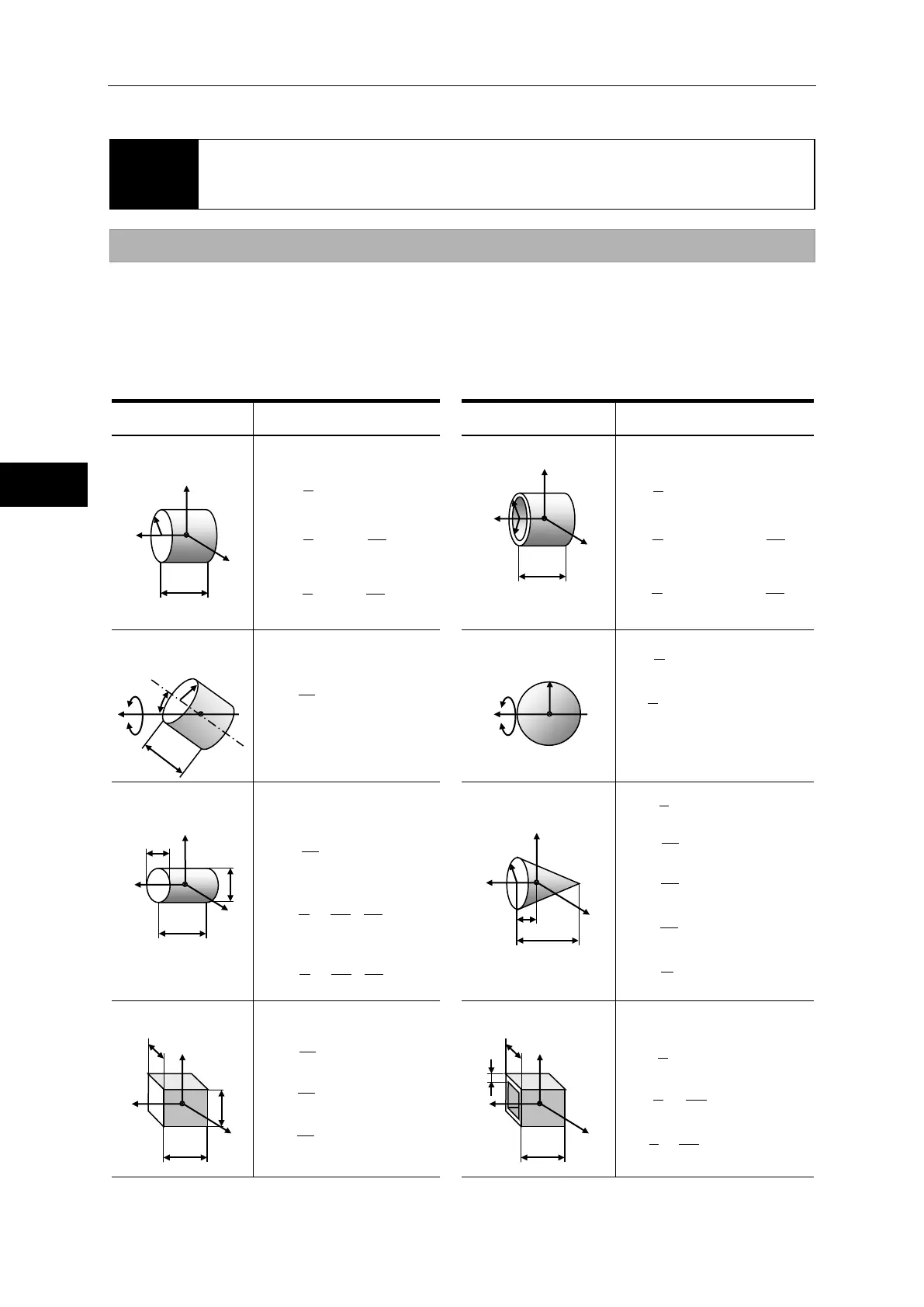
Shape of object
Mass, inertia, position of
center of gravity
Shape of object
Mass, inertia, position of
center of gravity
Circular cylinder
Round pipe
Tilted circular cylinder
Sphere
Elliptic circular cylinder
Cone
Prism
Regular square pipe
R
L
z
x
y
ρL
R
m
2
π
=
2
Rm
2
1
Ix
=








+=
3
L
Rm
4
1
Iy
2
2








+=
3
L
Rm
4
1
Iz
2
2
R
1
L
R
2
z
x
y
R
1
:Outside diameter
R
2
:Inside diameter
( )
ρπ LRRm
2
2
2
1
−=
(
)










++=
3
L
RRm
4
1
Iy
2
2
2
2
1
(
)
2
2
2
1
RRm
2
1
Ix +=
(
)










++=
3
L
RRm
4
1
Iz
2
2
2
2
1
B
L
z
x
y
C
(
)
22
CBm
16
1
Ix +=








+=
3
L
4
C
m
4
1
Iy
22








+=
3
L
4
B
m
4
1
Iz
22
R
L
z
x
y
G
2
Rm
10
3
Ix =
(
)
22
L4Rm
80
3
Iy +=
(
)
22
L4Rm
80
3
Iz +=
4
L
G =
z
x
y
C
B
A
ρABCm =
(
)
22
CBm
12
1
Ix +=
(
)
22
ACm
12
1
Iy +=
(
)
2
2
BAm
12
1
Iz +=
D
B
A
z
x
y
( )
ρ
D-B4AD=m
( ) { }
2
2
DD-Bm
3
1
Ix +=
( )






++=
2
2
2
DD-B
A
m
6
1
Iy
2
( )






++=
2
2
2
DD-B
A
m
6
1
Iz
2
ρL
Rm
2
π=
(
)
{ }
θθ
2222
sinLcos1
3R
m
12
1
I
++
×
=
θ
R
L
θ
R
ρπ
3
R
3
4
m =
2
Rm
5
2
I =
ρLBCm π=
ρL
2
R
3
m π
π
=
A