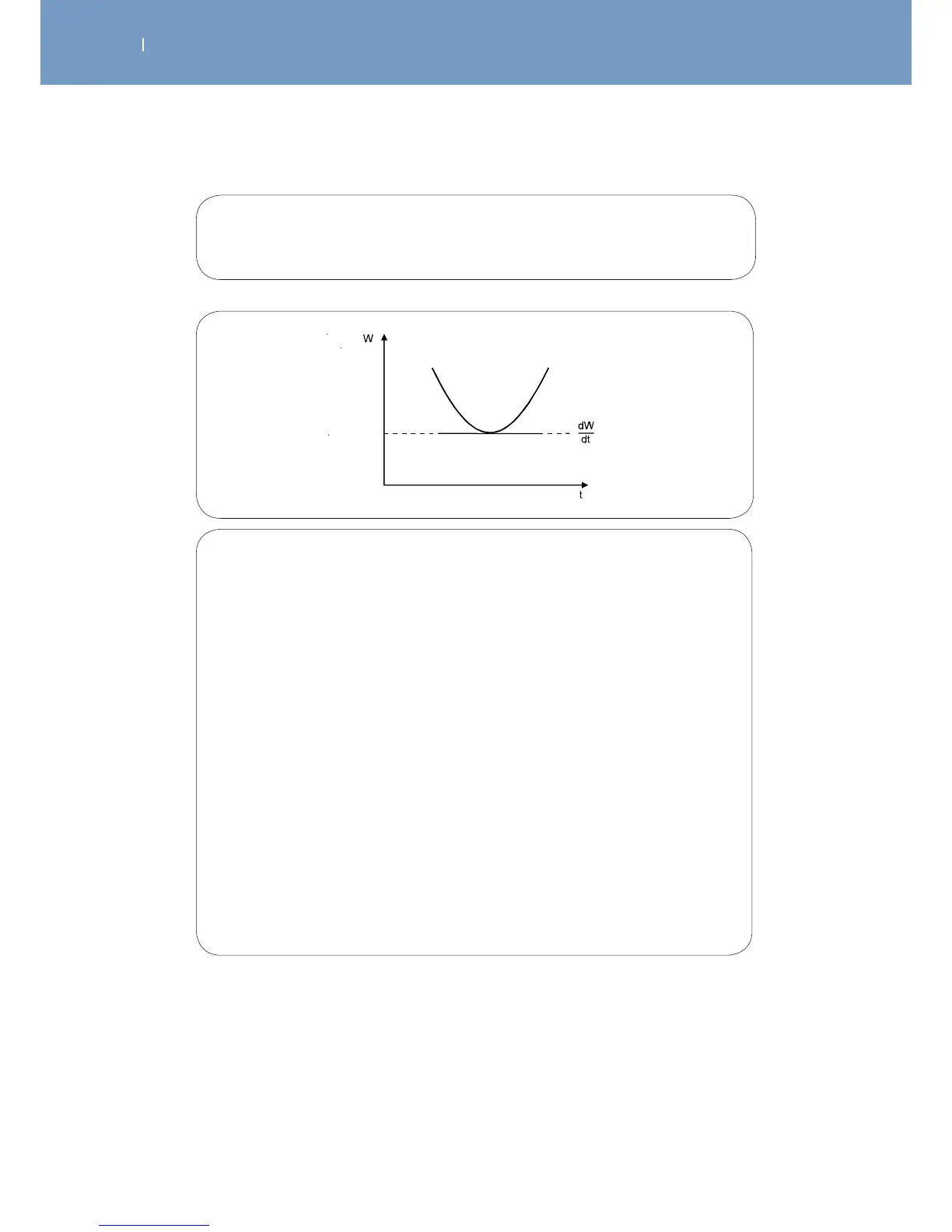
The electrical energy passing through the skin and tissue is minimal for duration of
the stimulation current, i.e. for a pulse duration, which is found by calculating the
derivative of the energy curve at the minimum energy point (Fig. 6).
Fig. 6
The derivative of 𝑊(
2
/𝑡+ 2 𝑖 + 𝑖
2
𝑡 𝑅 is 𝑑𝑤/𝑑𝑡 (
2
𝑡
2
+ 𝑖
2
𝑅
The derivative is the slope of the tangent at any point of a curve.
As at the minimum energy point, this slope is at zero since it is parallel to the abscissa,
we can therefore state that:
for 𝑊 𝑚𝑖𝑛𝑖𝑚𝑢𝑚 𝑑𝑤/𝑑𝑡 (
2
𝑡
2
+ 𝑖
2
𝑅= 0 therefore
2
𝑡
2
𝑅𝑖
2
𝑅𝑡
2
2
/𝑖
2
𝑡 /𝑖
As we have seen above, 𝑅 does not influence the determination of the pulse duration
corresponding to the minimum energy.
The electrical energy passing through the skin and tissue is therefore minimum when
the rectangular pulse duration is equal to /𝑖, which is in fact, as we have seen in the
article on the fundamental law of electrostimulation, the chronaxy value.
Furthermore, this is why, at the start of the century, pioneers in electrophysiology
chose the chronaxy as the value that characterises tissue excitability that is
independent from variations in skin resistance.
To reduce electrical energy to its minimum, the rectangular pulse duration will
therefore have to equal the chronaxy of the nerve structure that needs to be excited.
 Loading...
Loading...