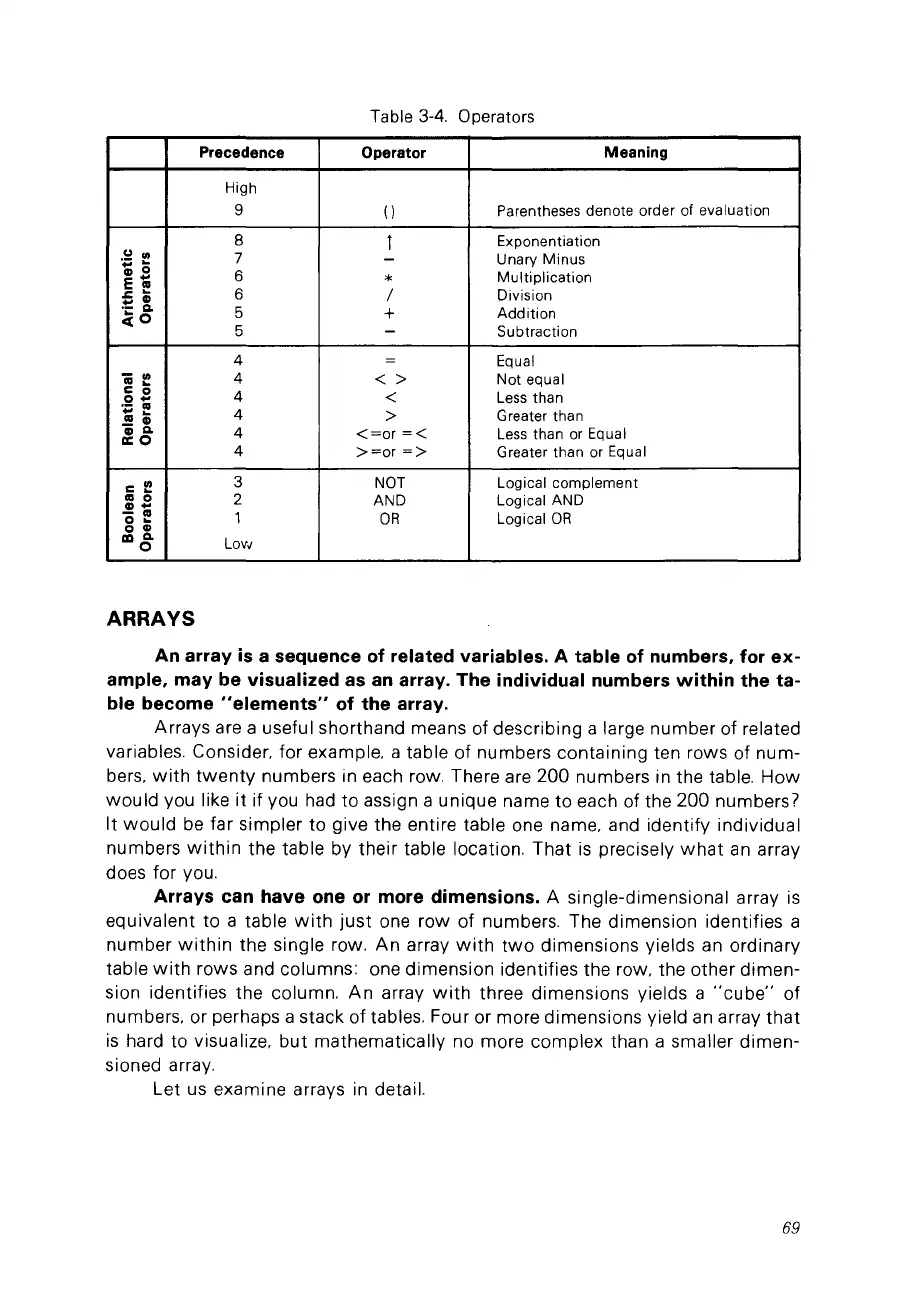
Table 3-4. Operators
Precedence Operator
Meaning
High
9
()
Parentheses denote order of evaluation
8
1
Exponentiation
~
~
7
-
Unary Minus
al
0
6
*
Multiplication
E'lii
~
...
6
/
Division
..
al
.-
a.
5
+
Addition
<0
5
-
Subtraction
4 =
Equal
- III
4
< >
Not equal
III ...
C 0
4
<
Less
than
0"
.-
III
Greater than
.....
4
>
.!!
al
al
a.
4
<=or
=<
Less
than or Equal
11:0
4
>=or
=>
Greater than or Equal
c
~
3
NOT Logical complement
III 0
2
AND Logical AND
al"
- III
1
OR
LogicalOR
o
...
o
al
IDa.
Law
0
ARRAYS
An array is a sequence of related variables. A table of numbers. for
ex-
ample.
may
be visualized as an array. The individual numbers
within
the ta-
ble become
"elements"
of the array.
Arrays are a useful shorthand means of describing a large number of related
variables. Consider, for example, a table of numbers containing ten rows of num-
bers,
with
twenty
numbers in each row. There are 200 numbers in the table.
How
would
vou like it if vou had
to
assign a unique name
to
each of the 200 numbers?
It
would
be
far simpler to give the entire table one name, and identify individual
numbers
within
the table by their table location. That
is
precisely
what
an array
does for vou.
Arrays can have one or more dimensions. A single-dimensional array
is
equivalent to a table
with
just
one row of numbers. The dimension identifies a
number
within
the single row.
An
array
with
two
dimensions yields
an
ordinary
table
with
rows and columns: one dimension identifies the row. the other dimen-
sion identifies the column.
An
array
with
three dimensions yields a
"cube"
of
numbers. or perhaps a stack of tables. Four or more dimensions yield
an
array
that
is
hard to visualize.
but
mathematically no more complex than a smaller dimen-
sioned array.
Let us examine arrays in detai!.
69

 Loading...
Loading...