Faro FaroArm P08 - Eulerian Angles

FaroArm User Guide
January 2007
28
Chapter 1: Introduction to the FaroArm
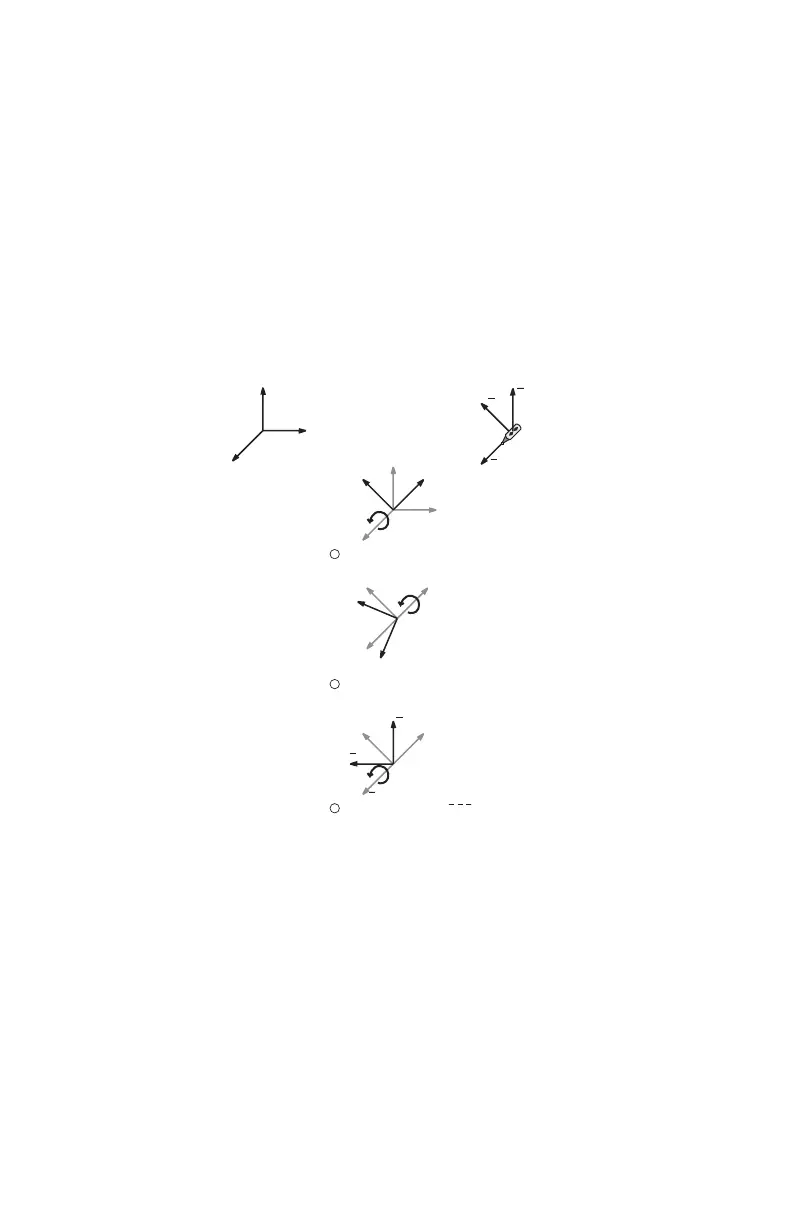
Eulerian Angles
Eulerian Angles define an orthogonal coordinate system that results
from three successive rotations from a fixed coordinate system.
The three successive rotations are:
A is a rotation about the Z-axis giving: X´,Y´,Z´ = A
B is a rotation about the X-axis giving: X´´,Y´´,Z´´ = B
C is a rotation about the Z-axis giving: X´´´,Y´´´,Z´´´= C
Direction cosines I, J, and K can be computed from two of three
Eulerian angles. The direction of these vectors are “in” to the part, or
“out” of the FaroArm probe.
I = (sin B sin A)
J = (-sin B cos A)
K = cos B
Figure 1-16 Eulerian Angles
Y
X
Z
Y
X
Z
Probe Coordinate System
Part Coordinate System
Y
X
Z
Y'
X'
Z'
A
1 Rotate "A" about Z Axis to yield X', Y', Z'
Y'
X'
Z'
Y''
X''
Z''
B
2 Rotate "B" about X' Axis to yield X'', Y'', Z''
Y''
X''
Z''
Y
X
Z
C
3 Rotate "C" about Z'' Axis to yield X, Y, Z
Note: All Rotations are
Counter Clockwise
08M46E00_FaroArmUSB.book Page 28 Monday, January 15, 2007 1:12 PM