To Next Page

To Previous Page

IQmath

IQmath Approach

bit

IQmath

Approach

y =

+ b

I8 Q24

I16 Q48

>> 24

Align Decimal

Point Of Multiply

I8 Q24

sssssssssssssssssI16 Q24

I8 Q24

Y = ((i64) M * (i64) X) >> Q + B;

in C:

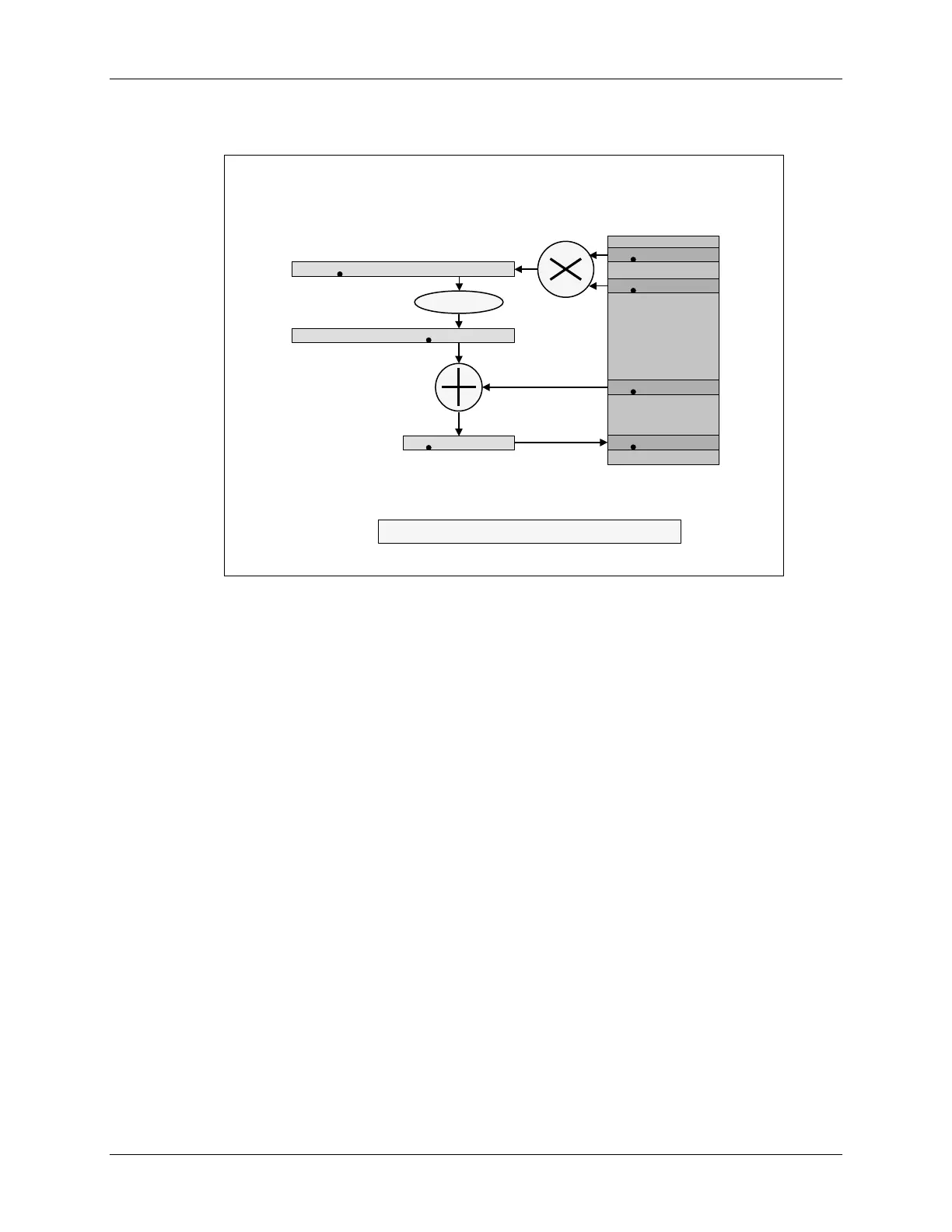
In the "IQmath" approach, rather then scaling the operands, which get added to or subtracted

from the multiplication result, we do the reverse. The multiplication result binary point is scaled

back such that it aligns to the operands, which are added to or subtracted from it. The C code

implementation of this is given by linear equation below:

int32 Y, M, X, B;

Y = ((int64) M * (int64) X) >> 24 + B;

The slide shows the implementation of the equation on a processor containing hardware that can

perform a 32x32 bit multiply, 32-bit addition/subtraction and 64-bit logical and arithmetic shifts

efficiently.

The key advantage of this approach is shown by what can then be done with the C and C++ com-

piler to simplify the coding of the linear equation example.

Lets take an additional step and create a multiply function in C that performs the following opera-

tion:

int32 _IQ24mpy(int32 M, int32 X) { return ((int64) M * (int64) X) >> 24; }

The linear equation can then be written as follows:

Y = _IQ24mpy(M , X) + B;

Already we can see a marked improvement in the readability of the linear equation.

C28x - Numerical Concepts & IQmath 8 - 19

Texas Instruments C28 Series Student Guide

Other manuals for Texas Instruments C28 Series