Tektronix MSO54B Printable Help

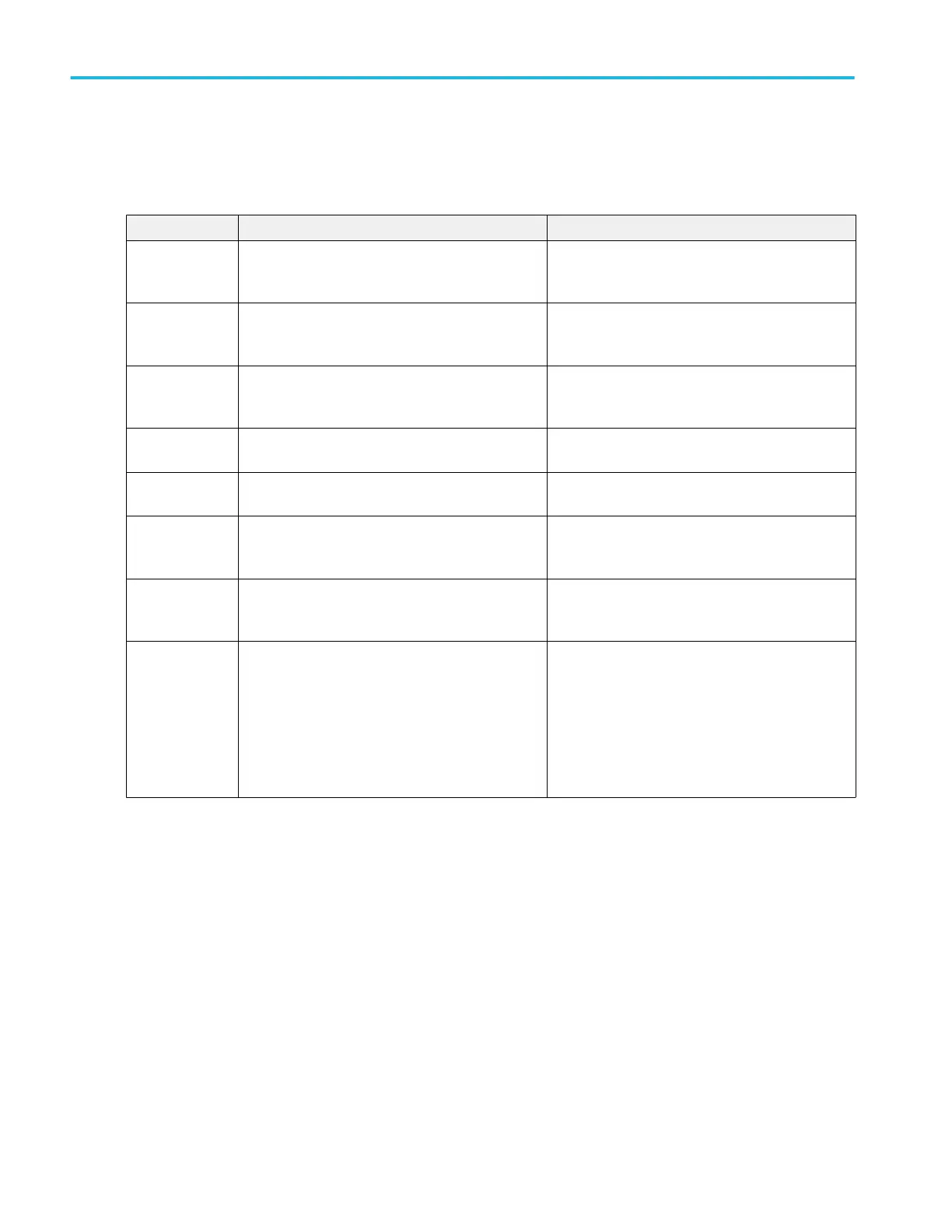
FFT windows. Each FFT window is a trade-off between frequency resolution and magnitude accuracy. What you want to
measure and your source signal characteristics help determine which window to use. Use the following guidelines to select the
best window.
FFT window Characteristics Best for measuring
Hanning Better frequency, poorer magnitude accuracy than
Rectangular. Hanning has slightly poorer frequency
resolution than Hamming.
Sine, periodic, and narrow-band random noise.
Transients or bursts where the signal levels before
and after the event are significantly different.
Rectangular Best frequency, worst magnitude resolution. This is
essentially the same as no window.
Transients or bursts where the signal levels before
and after the event are nearly equal. Equal-amplitude
sine waves with frequencies that are very close.
Hamming Better frequency, poorer magnitude accuracy than
Rectangular. Hamming has slightly better frequency
resolution than Hanning.
Sine, periodic, and narrow-band random noise.
Transients or bursts where the signal levels before
and after the event are significantly different.
Blackman-Harris Best magnitude, worst frequency resolution. Predominantly single frequency signals to look for
higher order harmonics.
Kaiser-Bessel Less spectral leakage than the Hanning, Hamming,
or Rectangular windows.
Predominantly single frequency signals to look for
higher order harmonics.
Gaussian The time-domain shape of an exponential Gaussian
function transforms into a Gaussian exponential
shape in the frequency domain.
Optimal localization in both the time and frequency
domain.
Flattop2 Wider resolution bandwidth but lower side lobe
attenuation. Also, it is unique because the time
domain shape has negative values.
Useful for high accuracy magnitude measurements
for signals that do not require very narrow bandwidth
TekExp The Tek Exponential window was invented at
Tektronix. In the time domain, it is not asymmetrical
bell shape as is the case with the other windows.
Instead, it is exponential with a peak at the 20%
position of the time domain gate. The frequency
domain shape is triangular. More of the acquired data
record length is used to capture the impulse
response.
Use this window for impulse-response testing where
the 20% position is the zero phase reference point.
You can also determine the best window empirically by first selecting the Rectangular window, and then selecting (in the
following order) the Hamming, Hanning, and Blackman-Harris windows until the frequency components merge. Use the window
just prior to where the frequencies emerge for the best compromise between resolution and amplitude accuracy.
Closing a plot view.
To close (delete) a Plot view, tap the X in the upper right corner of the view.
Deleting the Measurement badge that enabled the plot also closes the plot.
Menus and dialog boxes
322 MSO54, MSO56, MSO58, MSO58LP, MSO64 Help

Tektronix MSO54B Specifications

General

Brand	Tektronix
Model	MSO54B
Category	Test Equipment
Language	English