768 Appendix A: Functions and Instructions
BldData CATALOG
BldData
[
dataVar
]
Creates data variable
dataVar
based on the
information used to plot the current graph.
BldData
is valid in all graphing modes.
If
dataVar
is omitted, the data is stored in the system
variable
sysData
.
Note: The first time you start the Data/Matrix Editor
after using
BldData
,
dataVar
or
sysData
(depending
on the argument you used with
BldData
) is set as
the current data variable.
The incremental values used for any independent
variables (
x
in the example to the right) are
calculated according to the Window variable values.
For information about the increments used to
evaluate a graph, refer to the module that describes
that graphing mode.
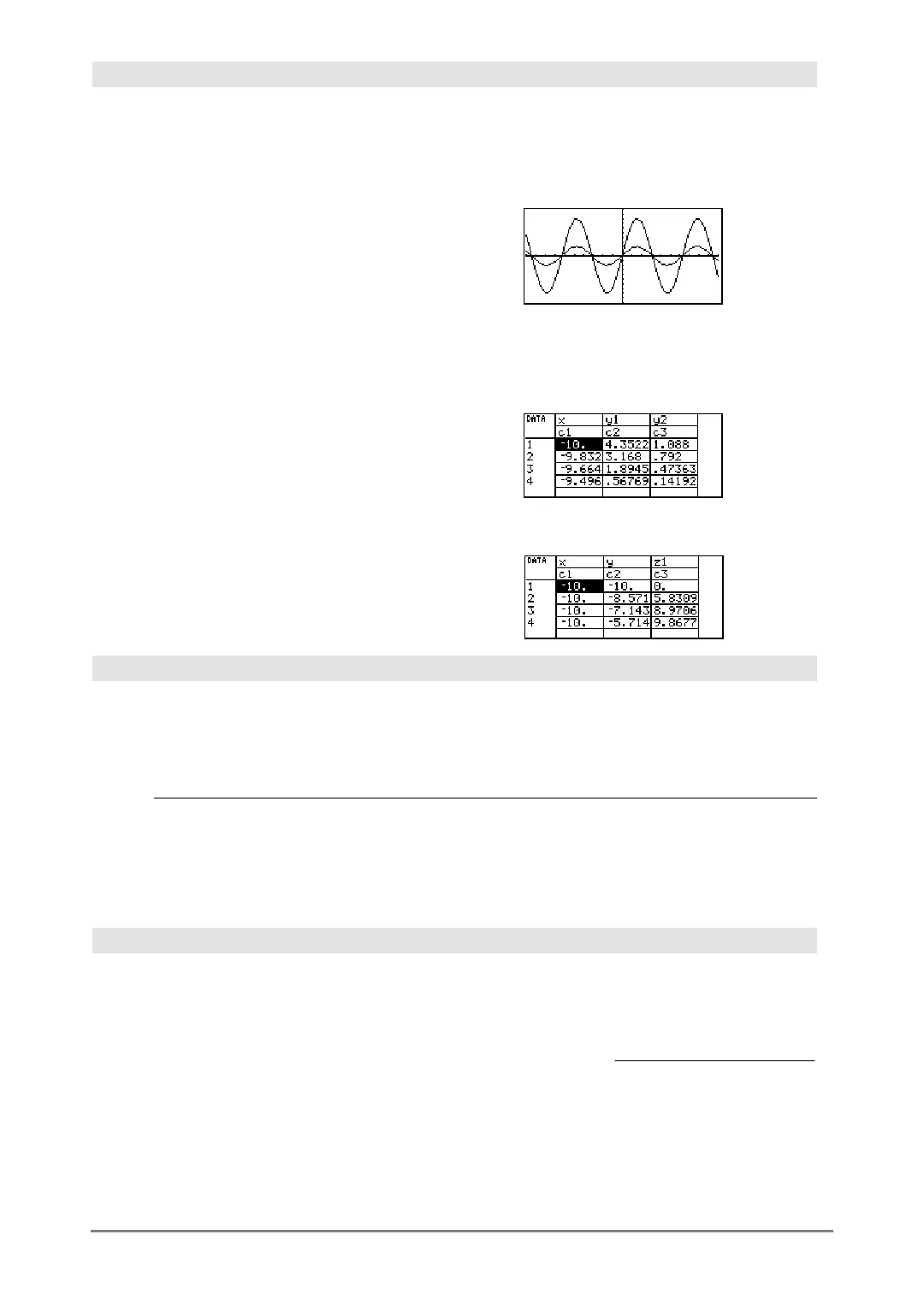
In function graphing mode and Radian angle
mode:
8ùsin(x)!y1(x) ¸ Done
2ùsin(x)!y2(x) ¸ Done
ZoomStd ¸
@ "
H ¥ "
BldData ¸ Done
O 6 ¸
3D graphing mode has two independent variables.
In the sample data to the right, notice that
x
remains
constant as
y
increments through its range of
values.
Then,
x
increments to its next value and
y
again
increments through its range. This pattern continues
until
x
has incremented through its range.
Note: The following sample data is from a 3D
graph.
ceiling() MATH/Number menu
ceiling(
expression1
) ⇒
integer
Returns the nearest integer that is
‚
the argument.
The argument can be a real or a complex number.
Note: See also
floor()
.
ceiling(0.456)
¸ 1.
ceiling(
list1
) ⇒
list
ceiling(
matrix1
) ⇒
matrix
Returns a list or matrix of the ceiling of each
element.
ceiling({ë3.1,1,2.5})
¸
{ë3. 1 3.}
ceiling([0,ë3.2
i
;1.3,4])
¸
[
0
2.
ë3.øi
4
]
cFactor() MATH/Algebra/Complex menu
cFactor(
expression1
[,
var
]) ⇒
expression
cFactor(
list1
[
,var
]) ⇒
list
cFactor(
matrix1
[
,var
]) ⇒
matrix
cFactor(
expression1
)
returns
expression1
factored
with respect to all of its variables over a common
denominator.
expression1
is factored as much as possible toward
linear rational factors even if this introduces new
non-real numbers. This alternative is appropriate if
you want factorization with respect to more than one
variable.
cFactor(a^3ùx^2+aùx^2+a^3+a)
¸
aø(a
+
ë
i
)ø(a
+
i
)ø(x
+
ë
i
)ø(x
+
i
)
cFactor(x^2+4/9)
¸
(3øx + ë2øi)ø(3øx + 2ø i)
9
cFactor(x^2+3)
¸ xñ
+
3
cFactor(x^2+a)
¸ xñ
+
a
 Loading...
Loading...











