778 Appendix A: Functions and Instructions
If you do not include any guesses and if any
equation is non-polynomial in any variable but all
equations are linear in all solution variables,
cSolve()
uses Gaussian elimination to attempt to
determine all solutions.
cSolve(u_+v_=
e
^(w_) and u_ì v_=
i
, {u_,v_}) ¸
u_=
e
w_
2
+1/2ø
i
and v_=
e
w_
ì
i
2
If a system is neither polynomial in all of its
variables nor linear in its solution variables,
cSolve()
determines at most one solution using an
approximate iterative method. To do so, the number
of solution variables must equal the number of
equations, and all other variables in the equations
must simplify to numbers.
cSolve(
e
^(z_)=w_ and w_=z_^2,
{w_,z_}) ¸
w_=.494… and z_=ë.703…
A non-real guess is often necessary to determine a
non-real solution. For convergence, a guess might
have to be rather close to a solution.
cSolve(
e
^(z_)=w_ and w_=z_^2,
{w_,z_=1+
i
}) ¸
w_=.149… + 4.891…ø
i
and
z_=1.588… + 1.540…ø
i
CubicReg MATH/Statistics/Regressions menu
CubicReg
list1
,
list2
[, [
list3
] [,
list4
,
list5
]]
Calculates the cubic polynomial regression and
updates all the statistics variables.
All the lists must have equal dimensions except for
list5
.
list1
represents xlist.
list2
represents ylist.
list3
represents frequency.
list4
represents category codes.
list5
represents category include list.
Note:
list1
through
list4
must be a variable name or
c1–c99 (columns in the last data variable shown in
the Data/Matrix Editor).
list5
does not have to be a
variable name and cannot be c1–c99.
In function graphing mode.
{0,1,2,3}! L1
¸ {0 1 2 3}
{0,2,3,4}! L2
¸ {0 2 3 4}
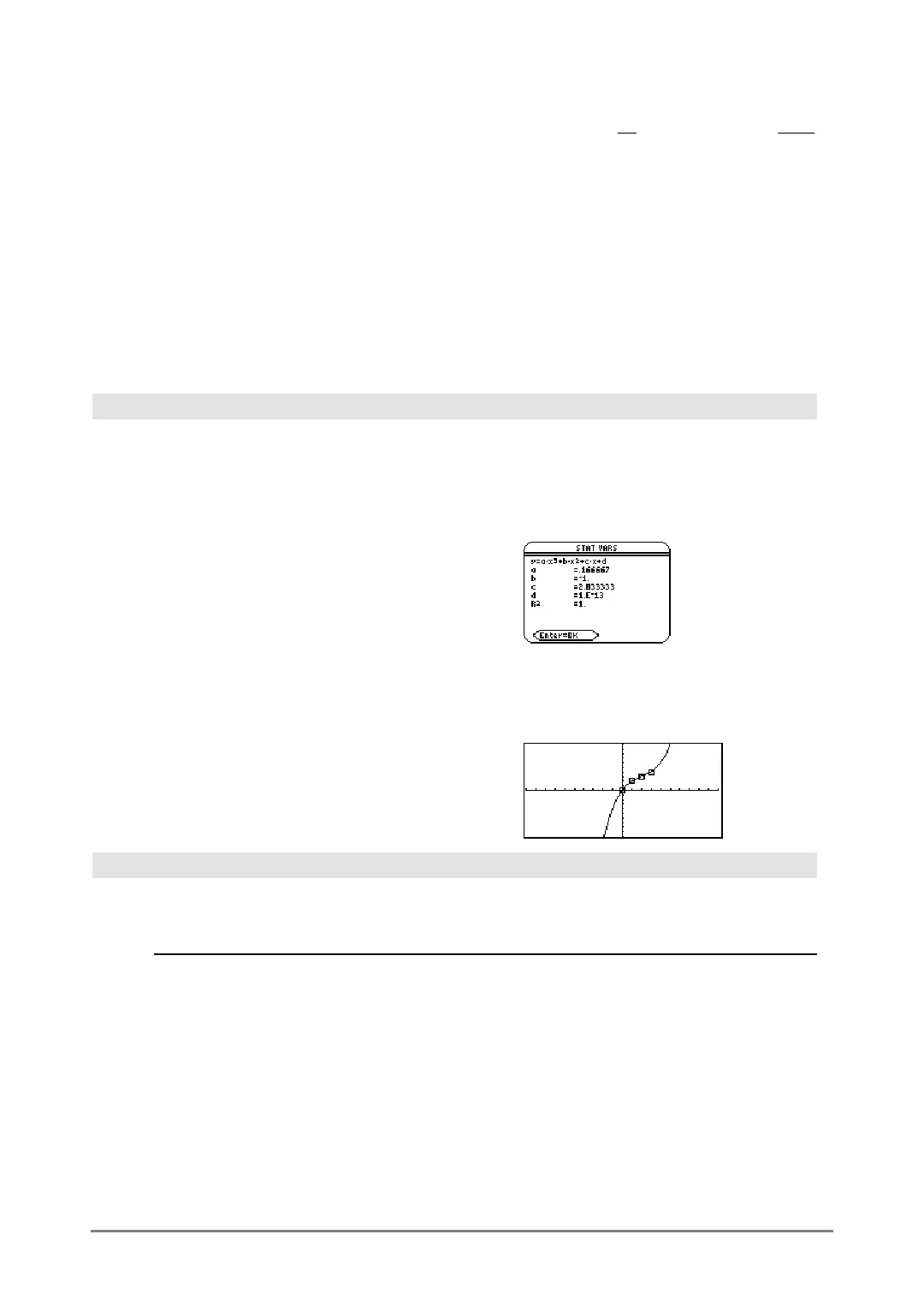
CubicReg L1,L2
¸ Done
ShowStat
¸
¸
regeq(x)"y1(x)
¸ Done
NewPlot 1,1,L1,L2
¸ Done
¥%
cumSum() MATH/List menu
cumSum(
list1
) ⇒
list
Returns a list of the cumulative sums of the
elements in
list1
, starting at element 1.
cumSum({1,2,3,4})
¸
{1 3 6 10}
cumSum(
matrix1
) ⇒
matrix
Returns a matrix of the cumulative sums of the
elements in
matrix1
. Each element is the cumulative
sum of the column from top to bottom.
[1,2;3,4;5,6]! m1
¸
1 2
3 4
5 6
cumSum(m1)
¸
1 2
4 6
9 12
To Next Page
Loading...
Need help?
General
