Appendix A: Functions and Instructions 795
ExpReg MATH/Statistics/Regressions menu
ExpReg
list1, list2
[, [
list3
] [,
list4, list5
]]
Calculates the exponential regression and updates
all the system statistics variables.
All the lists must have equal dimensions except for
list5
.
list1
represents xlist.
list2
represents ylist.
list3
represents frequency.
list4
represents category codes.
list5
represents category include list.
Note:
list1
through
list4
must be a variable name or
c1–c99 (columns in the last data variable shown in
the Data/Matrix Editor).
list5
does not have to be a
variable name and cannot be c1–c99.
In function graphing mode:
{1,2,3,4,5,6,7,8}! L1
¸
{1 2
...
}
{1,2,2,2,3,4,5,7}! L2
¸
{1 2
...
}
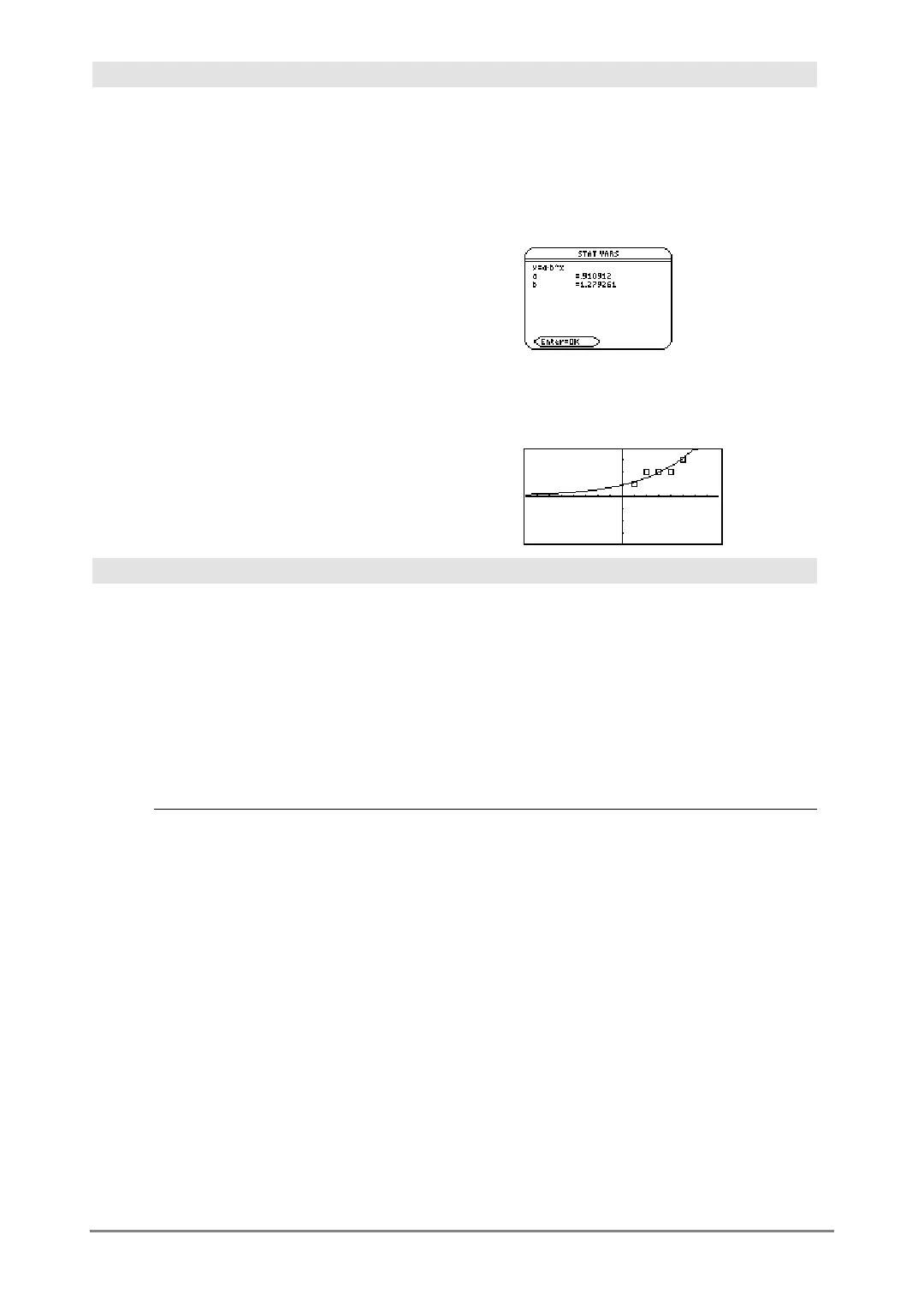
ExpReg L1,L2
¸ Done
ShowStat
¸
¸
Regeq(x)"y1(x)
¸ Done
NewPlot 1,1,L1,L2
¸ Done
¥%
factor() MATH/Algebra menu
factor(
expression1
[,
var
]) ⇒
expression
factor(
list1
[
,var
]) ⇒
list
factor(
matrix1
[
,var
]) ⇒
matrix
factor(
expression1
) returns
expression1
factored with
respect to all of its variables over a common
denominator.
expression1
is factored as much as possible toward
linear rational factors without introducing new non-
real subexpressions. This alternative is appropriate
if you want factorization with respect to more than
one variable.
factor(a^3ù x^2ì aù x^2ì a^3+a)
¸
aø(a
ì1)ø(a
+
1)ø(x
ì1)ø(x
+
1)
factor(x^2+1)
¸ xñ +
1
factor(x^2ì 4)
¸ (x
ì 2)ø (x
+
2)
factor(x^2ì 3)
¸ xñì3
factor(x^2ì a)
¸ xñìa
factor(
expression1,var
)
returns
expression1
factored
with respect to variable
var
.
expression1
is factored as much as possible toward
real factors that are linear in
var
, even if it introduces
irrational constants or subexpressions that are
irrational in other variables.
The factors and their terms are sorted with
var
as
the main variable. Similar powers of
var
are
collected in each factor. Include
var
if factorization is
needed with respect to only that variable and you
are willing to accept irrational expressions in any
other variables to increase factorization with respect
to
var
. There might be some incidental factoring with
respect to other variables.
factor(a^3ù x^2ì aù x^2ì a^3+a,x)
¸
aø (añì1)ø (x
ì 1)ø (x
+
1)
factor(x^2ì 3,x)
¸
(x
+
‡3)ø (x
ì ‡3)
factor(x^2ì a,x)
¸
(x
+
‡a)ø (x
ì ‡a)

 Loading...
Loading...











