868 Appendix A: Functions and Instructions
zeros() MATH/Algebra menu
zeros(
expression
,
var
) ⇒
list
Returns a list of candidate real values of
var
that
make
expression
=0.
zeros()
does this by computing
exp8list(solve(
expression
=0,
var
)
,var
)
.
zeros(aù x^2+bù x+c,x)
¸
{
ë( bñ-4øaøc-+b)
2øa
bñ-4øaøc-b
2øa
}
aù x^2+bù x+c|x=ans(1)[2]
¸ 0
For some purposes, the result form for
zeros()
is
more convenient than that of
solve()
. However, the
result form of
zeros()
cannot express implicit
solutions, solutions that require inequalities, or
solutions that do not involve
var
.
Note: See also
cSolve()
,
cZeros()
, and
solve()
.
exact(zeros(aù (
e
^(x)+x)
(sign (x)ì 1),x))
¸ {}
exact(solve(aù (
e
^(x)+x)
(sign (x)ì 1)=0,x))
¸
e
x
+
x
=
0 or x>0 or a
=
0
zeros({
expression1
,
expression2
}, {
varOrGuess1
,
varOrGuess2
[
,
…
]
}) ⇒
matrix
Returns candidate real zeros of the simultaneous
algebraic
expressions
, where each
varOrGuess
specifies an unknown whose value you seek.
Optionally, you can specify an initial guess for a
variable. Each
varOrGuess
must have the form:
variable
– or –
variable
=
real
or
non
-
real
number
For example,
x
is valid and so is
x=3
.
If all of the expressions are polynomials and if you
do NOT specify any initial guesses,
zeros()
uses
the lexical Gröbner/Buchberger elimination method
to attempt to determine all real zeros.
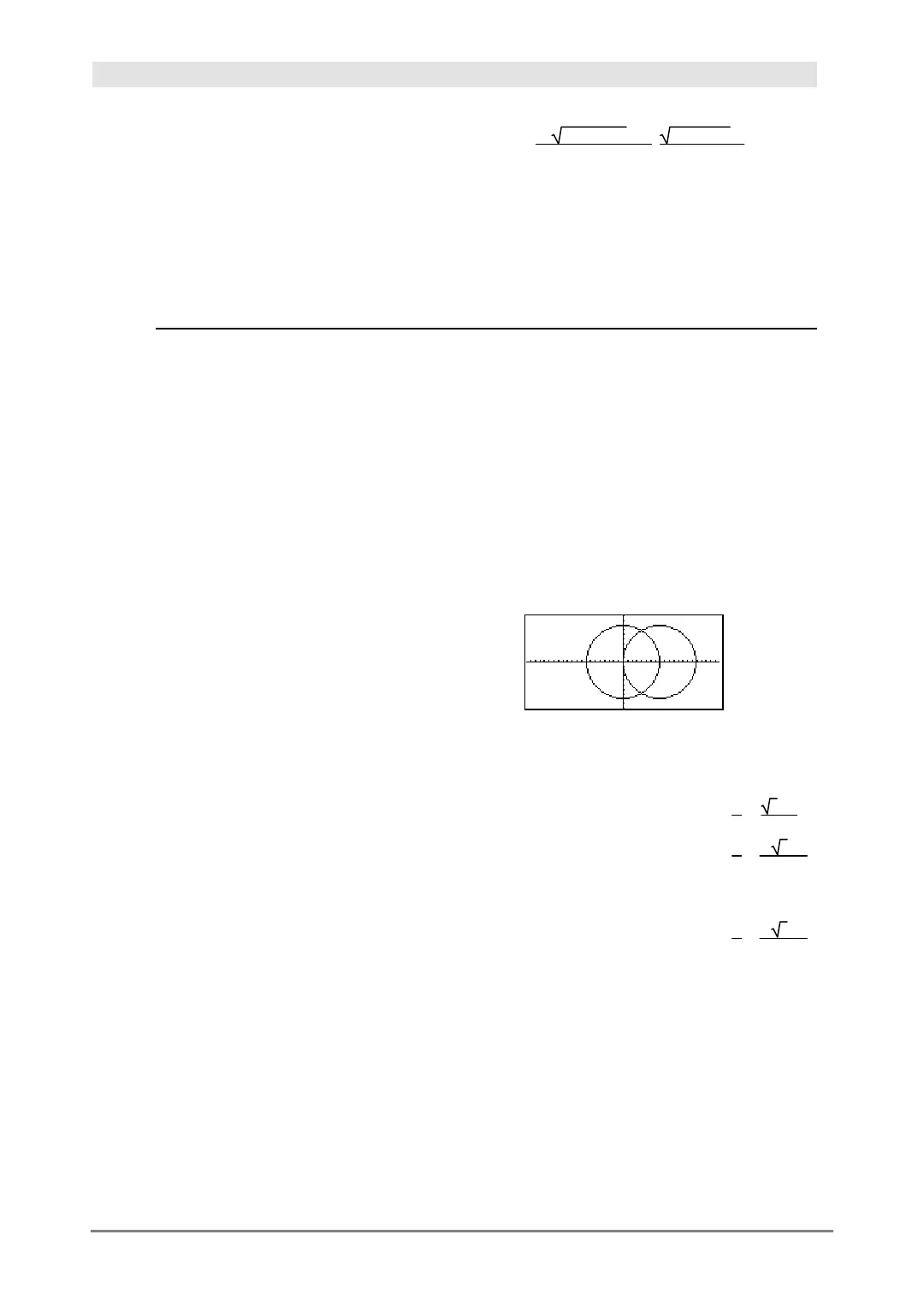
For example, suppose you have a circle of radius r
at the origin and another circle of radius r centered
where the first circle crosses the positive x-axis.
Use
zeros()
to find the intersections.
As illustrated by r in the example to the right,
simultaneous
polynomial
expressions can have
extra variables that have no values, but represent
given numeric values that could be substituted later.
Each row of the resulting matrix represents an
alternate zero, with the components ordered the
same as the
varOrGuess
list. To extract a row, index
the matrix by [
row
].
zeros({x^2+y^2ì r^2,
(xì r)^2+y^2ì r^2},{x,y}) ¸
r
2
3ør
2
r
2
ë
3ør
2
Extract row 2:
ans(1)[2] ¸
r
2
ë
3ør
2
To Next Page
Loading...
Need help?
General
