HP 50G - Fourier Series; Function FOURIER

Page 14-5
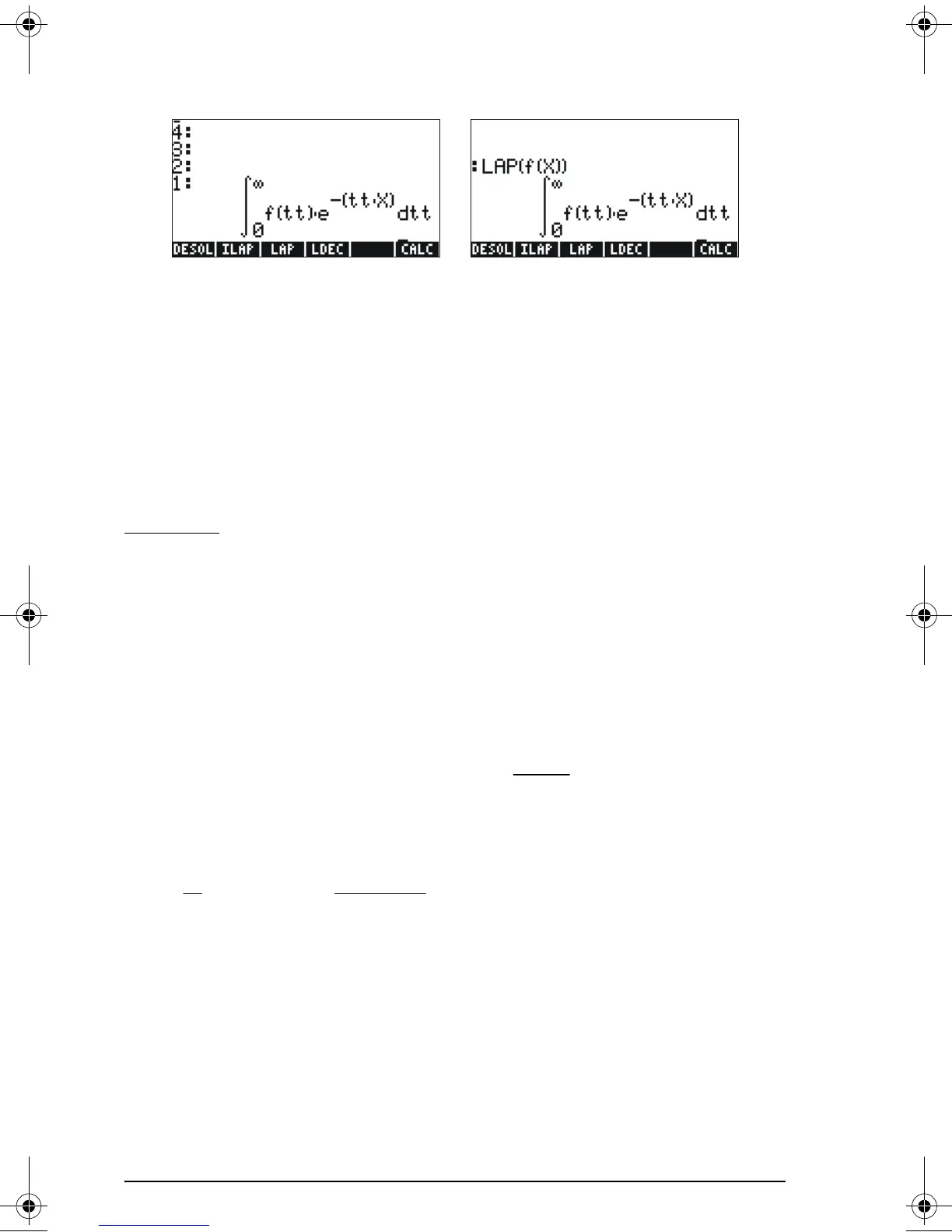
Compare these expressions with the one given earlier in the definition of
the Laplace transform, i.e.,
and you will notice that the CAS default variable X in the equation writer
screen replaces the variable s in this definition. Therefore, when using the
function LAP you get back a function of X, which is the Laplace transform of
f(X).
Example 2 – Determine the inverse Laplace transform of F(s) = sin(s). Use:
‘1/(X+1)^2’`ILAP
The calculator returns the result: ‘X⋅e
-X
’, meaning that L
-1
{1/(s+1)
2
} =
x⋅e
-x
.
Fourier series
A complex Fourier series is defined by the following expression
where
Function FOURIER
Function FOURIER provides the coefficient c
n
of the complex-form of the
Fourier series given the function f(t) and the value of n. The function
FOURIER requires you to store the value of the period (T) of a T-periodic
function into the CAS variable PERIOD before calling the function. The
function FOURIER is available in the DERIV sub-menu within the CALC
menu (
„Ö).
{}
∫
∞
−
⋅==
0
,)()()(
dtetfsFtfL
st
∑
+∞
−∞=
⋅=
n
n
T
tin
ctf ),
2
exp()(
π
∫
∞−−−∞=⋅⋅
⋅⋅⋅
⋅=
T
n
ndtt
T
ni
tf
T
c
0
.,...2,1,0,1,2,...,,)
2
exp()(
1
π
SG49A.book Page 5 Friday, September 16, 2005 1:31 PM