Page 4-1
Chapter 4
Calculations with complex numbers
This chapter shows examples of calculations and application of functions to
complex numbers.
Definitions
A complex number z is a number z = x + iy, where x and y are real
numbers, and i is the imaginary unit defined by i² = –1. The complex
number x + iy has a real part, x = Re(z), and an imaginary part, y = Im(z).
The complex number z = zx + iy is often used to represent a point P(x,y) in
the x–y plane, with the x-axis referred to as the real axis, and the y-axis
referred to as the imaginary axis.
A complex number in the form x + iy is said to be in a rectangular
representation. An alternative representation is the ordered pair z = (x,y).
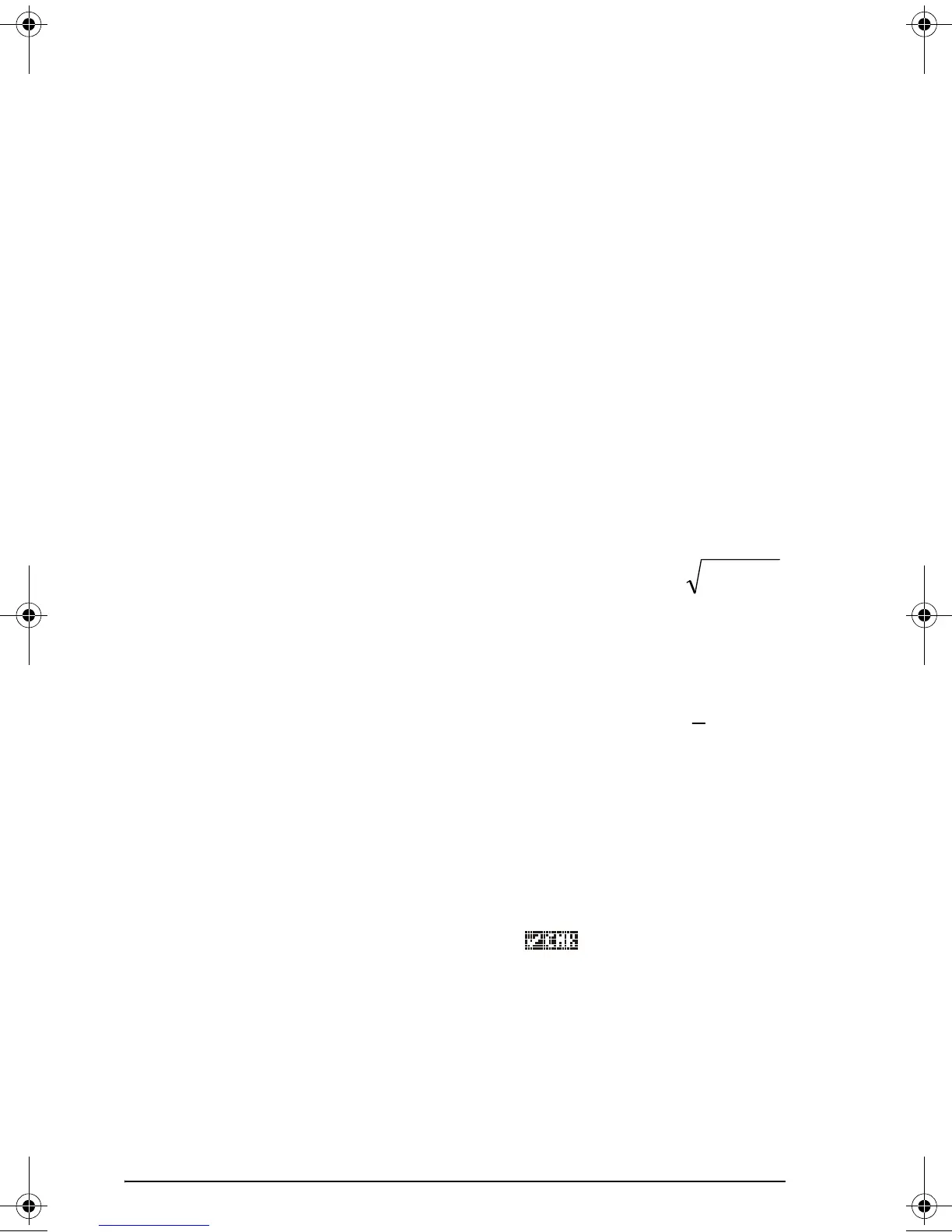
A complex number can also be represented in polar coordinates (polar
representation) as z = re
i
θ
= r·cosθ + i r·sinθ, where r = |z| =
is the magnitude of the complex number z, and θ = Arg(z) = arctan(y/x) is
the argument of the complex number z.
The relationship between the Cartesian and polar representation of
complex numbers is given by the Euler formula: ei
i
θ
= cosθ + i sinθ. The
complex conjugate of a complex number (z = x + iy = re
i
θ
) is = x – iy
= re
–
i
θ
. The complex conjugate of i can be thought of as the reflection of
z about the real (x) axis. Similarly, the negative of z, –z = –x –iy = –re
i
θ
,
can be thought of as the reflection of z about the origin.
Setting the calculator to COMPLEX mode
To work with complex numbers select the CAS complex mode:
H)@@CAS@ ˜˜™
The COMPLEX mode will be selected if the CAS MODES screen shows the
option _Complex checked, i.e.,
22
yx +
z
SG49A.book Page 1 Friday, September 16, 2005 1:31 PM
To Next Page
Loading...
Need help?
General
Weight and Dimensions
