Page 16-16
An interpretation for the integral above, paraphrased from Friedman (1990),
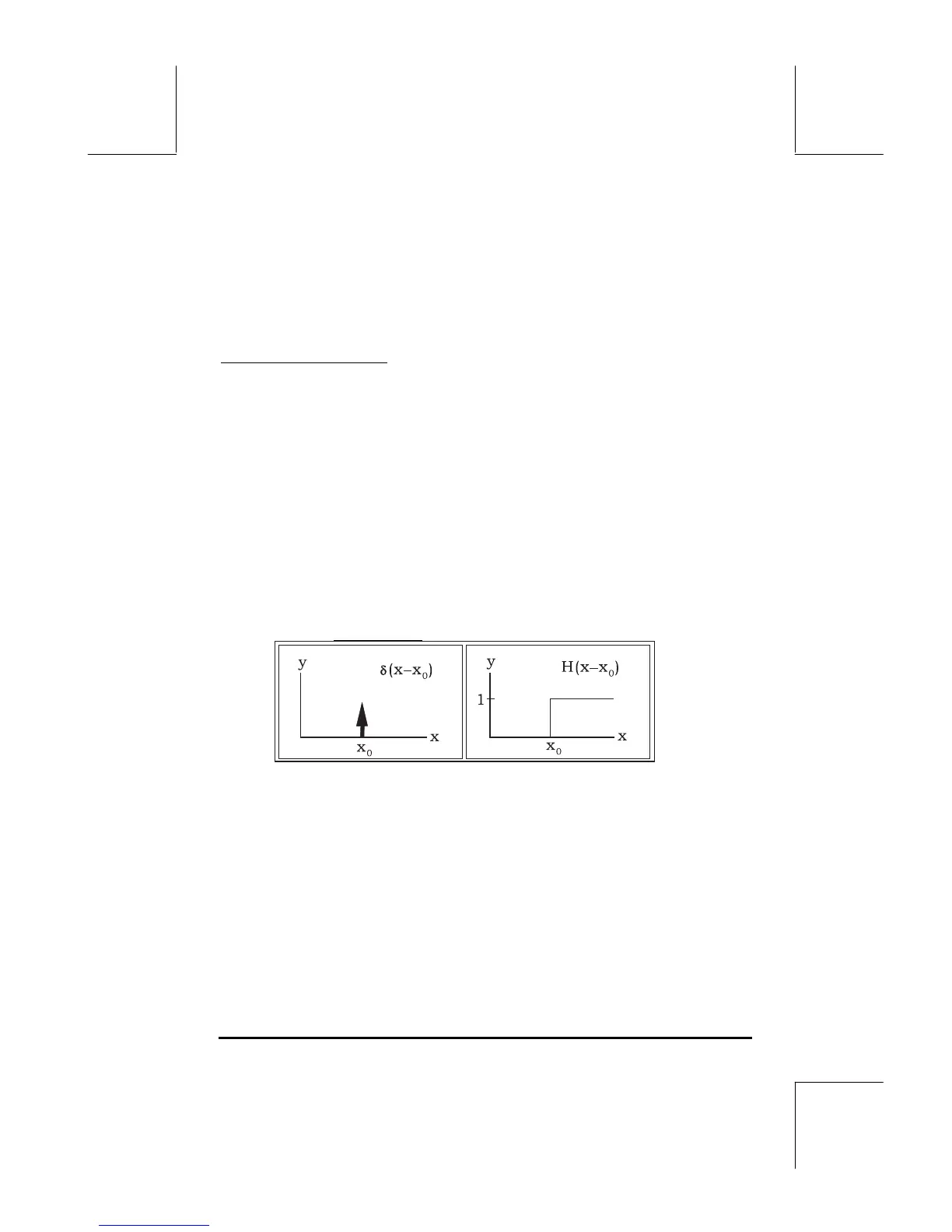
is that the δ-function “picks out” the value of the function f(x) at x = x
0
. Dirac’s
delta function is typically represented by an upward arrow at the point x = x0,
indicating that the function has a non-zero value only at that particular value
of x
0
.
Heaviside’s step function
, H(x), is defined as
<
>
=
0,0
0,1
)(
x
x
xH
Also, for a continuous function f(x),
Dirac’s delta function and Heaviside’s step function are related by dH/dx =
δ(x). The two functions are illustrated in the figure below.
You can prove that L{H(t)} = 1/s,
from which it follows that L{U
o
⋅H(t)} = U
o
/s,
where U
o
is a constant. Also, L
-1
{1/s}=H(t),
and L
-1
{ U
o
/s}= U
o
⋅H(t).
Also, using the shift theorem for a shift to the right, L{f(t-a)}=e
–as
⋅L{f(t)} =
e
–as
⋅F(s), we can write L{H(t-k)}=e
–ks
⋅L{H(t)} = e
–ks
⋅(1/s) = (1/s)⋅e
–ks
.
∫∫
∞
∞−
∞
=−
0
.)()()(
0
x
dxxfdxxxHxf

 Loading...
Loading...