Page 16-62
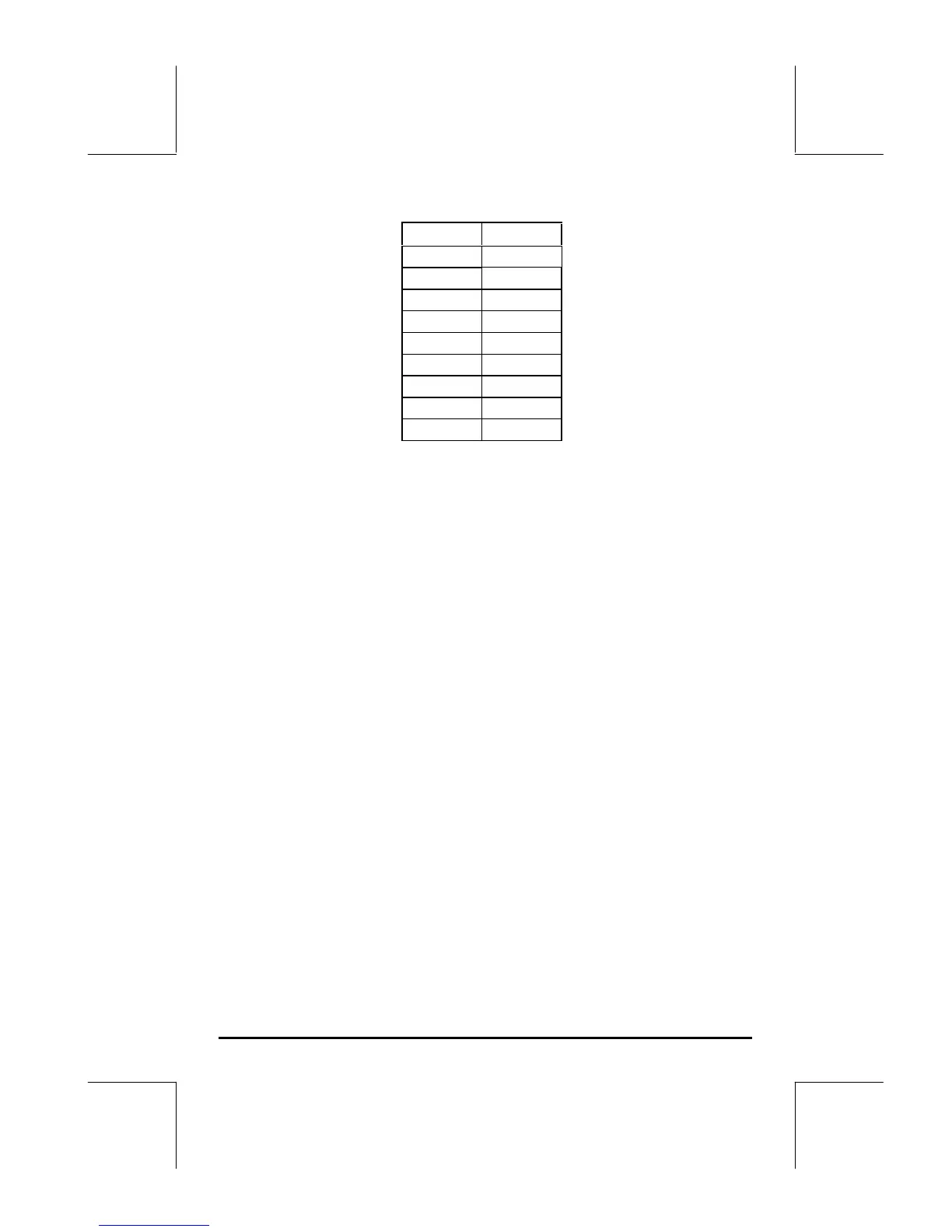
0.00 4.000
0.25 3.285
0.50 2.640
0.75 2.066
1.00 1.562
1.25 1.129
1.50 0.766
1.75 0.473
2.00 0.250
Graphical solution of first-order ODE
When we can not obtain a closed-form solution for the integral, we can
always plot the integral by selecting Diff Eq in the TYPE field of the PLOT
environment as follows: suppose that we want to plot the position x(t) for a
velocity function v(t) = exp(-t
2
), with x = 0 at t = 0. We know there is no
closed-form expression for the integral, however, we know that the definition
of v(t) is dx/dt = exp(-t
2
).
The calculator allows for the plotting of the solution of differential equations of
the form Y'(T) = F(T,Y). For our case, we let Y = x and T = t, therefore, F(T,Y)
= f(t, x) = exp(-t
2
). Let's plot the solution, x(t), for t = 0 to 5, by using the
following keystroke sequence:
• „ô (simultaneously, if in RPN mode) to enter PLOT environment
• Highlight the field in front of TYPE, using the —˜keys. Then, press
@CHOOS, and highlight Diff Eq, using the —˜keys. Press @@OK@@.
• Change field F: to ‘EXP(- t^2)’
• Make sure that the following parameters are set to: H-VAR: 0, V-VAR:
1
• Change the independent variable to t .
• Accept changes to PLOT SETUP: L @@OK@@
• „ò (simultaneously, if in RPN mode). To enter PLOT WINDOW
environment
• Change the horizontal and vertical view window to the following settings:
H-VIEW: -1 5; V-VIEW: -1 1.5
t v

 Loading...
Loading...