Omron R6Y Series User Manual

3-28
CHAPTER 3 Installation
6-2 Equation for moment of inertia calculation
Usually the R axis load is not a simple form, and the calculation of the moment
of inertia is not easy.
As a method, the load is replaced with several factors that resemble a simple
form for which the moment of inertia can be calculated. The total of the mo-
ment of inertia for these factors is then obtained.
The objects and equations often used for the calculation of the moment of iner-
tia are shown below. Incidentally, there is the following relation:
J (kgf·cm·sec
2
) = I (kgm
2
) × 10.2.
1) Moment of inertia for material particle
The equation for the moment of inertia for a material particle that has a ro-
tation center such as shown in Fig. 3-79 is as follows:
This is used as an approximate equation when x is larger than the object
size.
x
J=
Wx
g
2
(kgf · cm · sec
2
)
g : Gravitational acceleration (cm/sec
2
)
m : Mass of material particle (kg)
... (Eq. 3.1)
I= mx
2
(kgm
2
)
W : Weight of material particle (kgf)
Fig. 3-28
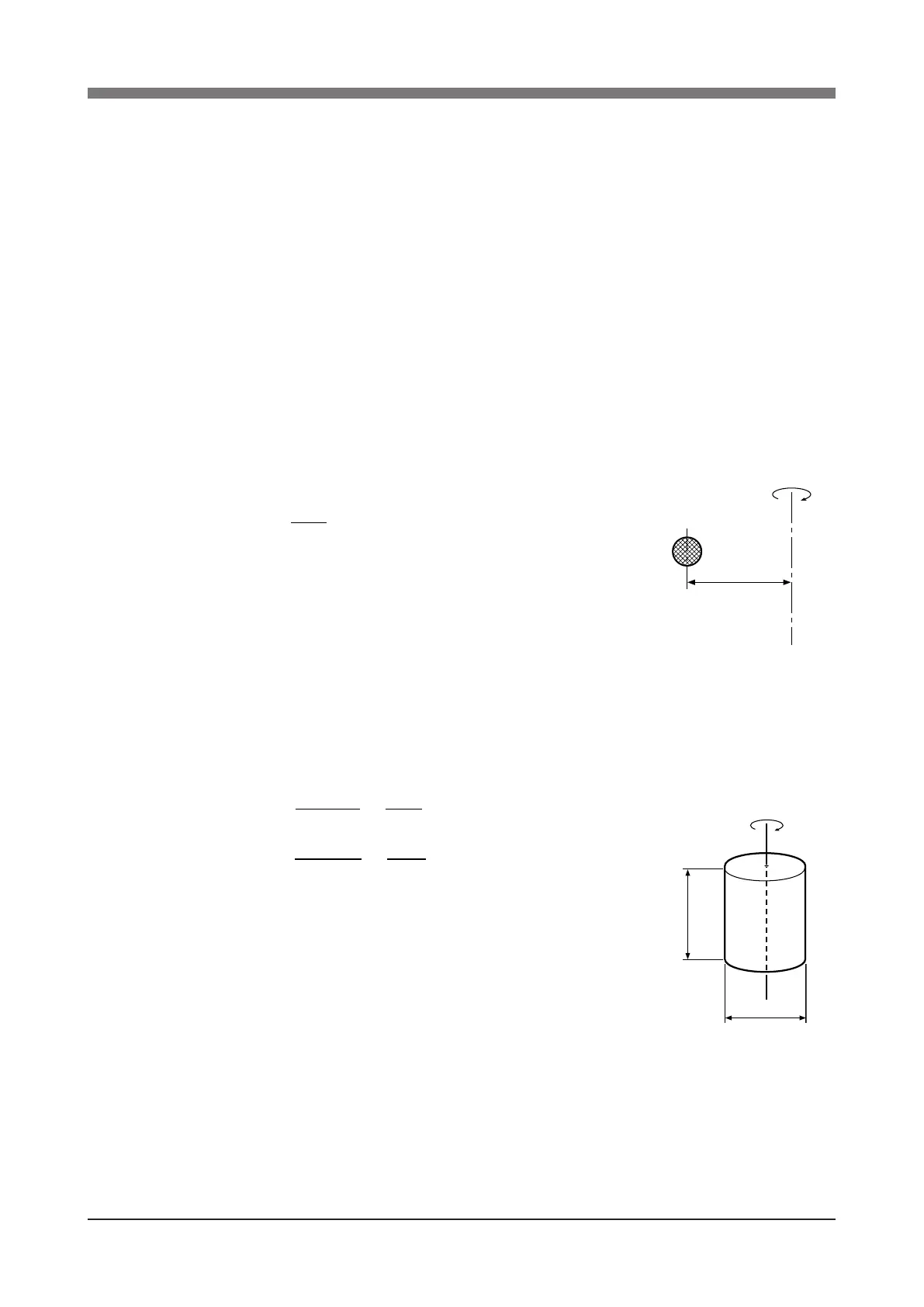
2) Moment of inertia for cylinder (part 1)
The equation for the moment of inertia for a cylinder that has a rotation
center such as shown in Fig. 3-80 is given below.
D
h
J=
ρπ D h
32g
WD
8g
=
4 2
(kgf · cm · sec
2
)
... (Eq. 3.2)
I=
ρπ D h
32
mD
8
=
4 2
(kgm
2
)
ρ : Density (kg/m
3
, kg/cm
3
)
g : Gravitational acceleration (cm/sec
2
)
m : Mass of cylinder (kg)
W : Weight of cylinder (kgf)
Fig. 3-29

Omron R6Y Series Specifications

General

Brand	Omron
Model	R6Y Series
Category	Robotics
Language	English