UFactory xArm6 User Manual

9
Roll/Pitch/Yaw
A
Y
ˆ
by β, and finally around
A
Z
ˆ
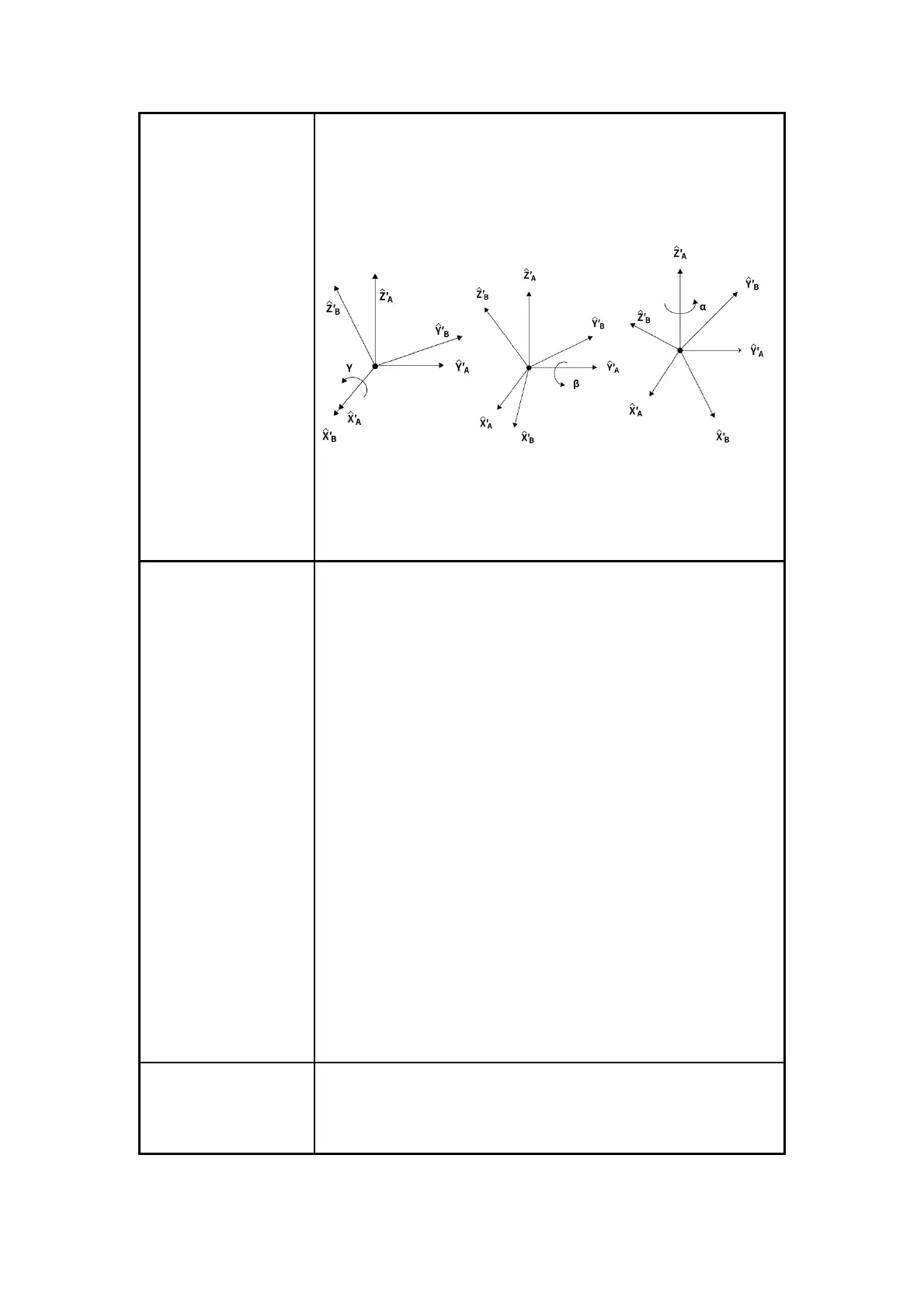
by α.
Each rotation is around a fixed axis of the reference coordinate system {A}. This
method is called the XYZ fixed angle coordinate system, and sometimes they
are defined as the roll angle, pitch angle, and yaw angle.
The above description is shown in the following figure:
The equivalent rotation matrix is:
       

XYZXYZ
A
B
RRRR ,,
Note: γ corresponds to roll; β corresponds to pitch; α corresponds to yaw.
Axis-Angle
Rx / Ry / Rz representation also, using 3 values to represent the pose (but not
three rotation angles), which is the product of a three-dimensional rotation
vector [x, y, z] and a rotation angle[phi (scalar)].
The characteristics of the axis angle:
Assume the rotation axis is [x , y, z], and the rotation angle is phi.
Then the representation of the axial angle:
[Rx, Ry, Rz] = [x * phi, y * phi, z * phi]
Note:
1. [x, y, z] is a unit vector, and phi is a non-negative value.
2. The vector length (modulus) of [Rx, Ry, Rz] can be used to estimate the
rotation angle, and the vector direction is the rotation direction.
3. If you want to express reverse rotation, invert the rotation axis vector [x, y, z],
and the value of phi remains unchanged.
4. Using phi and [x, y, z] can also derive the attitude representation as unit
quaternion q = [cos (phi / 2), sin (phi / 2) * x, sin (phi / 2) * y, sin (phi / 2) * z].
For example:
The vector of the rotation axis represented by the base coordinate system is [1,
0, 0], and the rotation angle is 180 degrees (π), then the axis angle representation
of this pose is [π, 0, 0].
The rotation axis is [0.707, 0.707, 0] and the rotation angle is 90 degrees (π / 2),
then the axis angle posture is [0.707 * (π / 2), 0.707 * (π / 2), 0].
The Base Coordinate
System
(please refer to the figure 1)
The base coordinate system is a Cartesian coordinate system based on the
mounting base of the robotic arm and used to describe the motion of the robotic
arm.
(front and back: X axis, left and right: Y axis, up and down: Z axis)

UFactory xArm6 Specifications

General

Brand	UFactory
Model	xArm6
Category	Robotics
Language	English