© 2019 Thorlabs GmbH
8 Tutorial
62
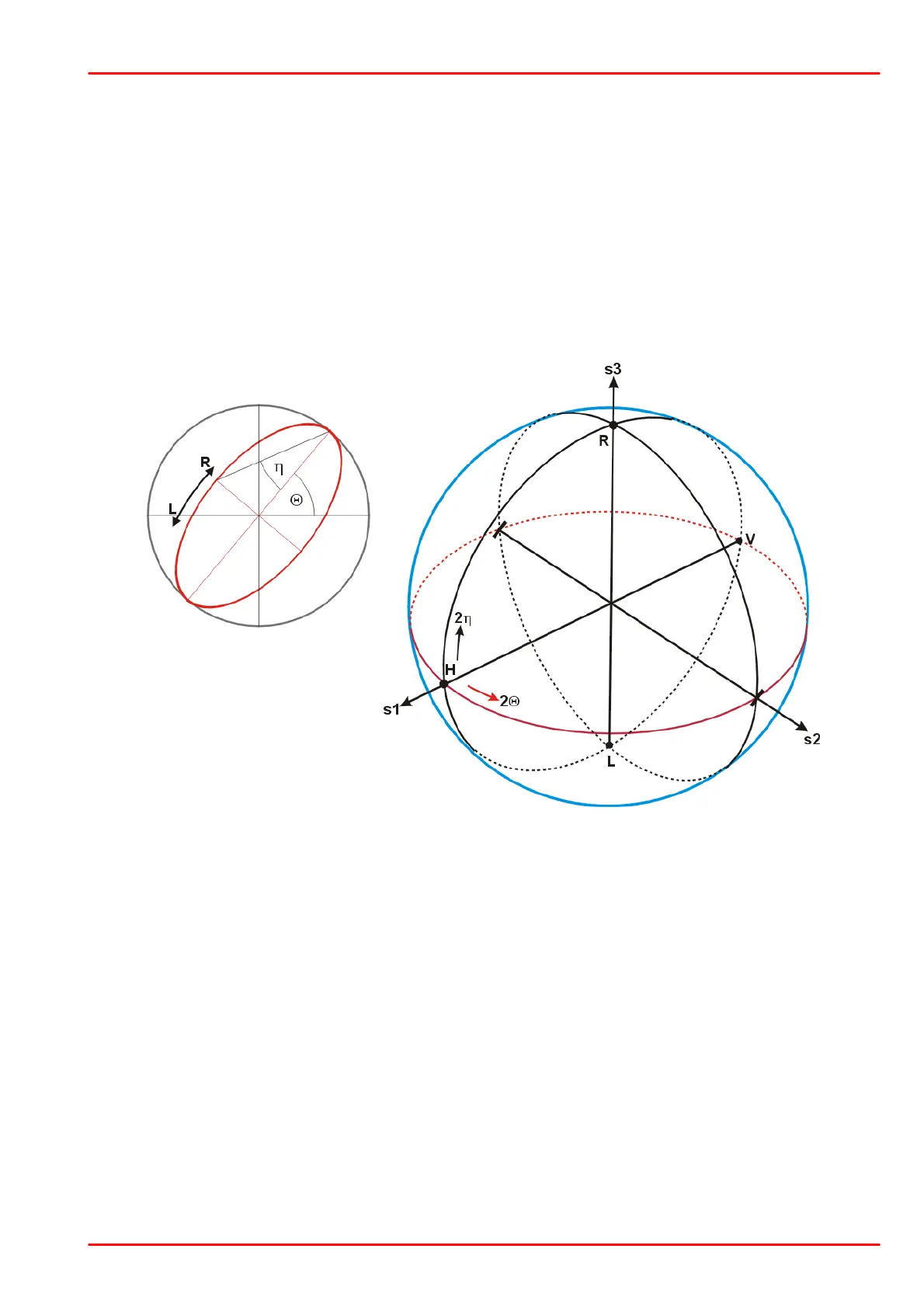
8.1.5 Poincaré Sphere
An appropriate way to display the state of polarization is the Poincaré sphere representation.
The center of the Poincaré sphere is located in the origin of a Cartesian coordinate system.
Any point on the surface of the Poincaré sphere is uniquely represented by its Cartesian co-
ordinates, also known as the 3 normalized Stokes Parameters s1, s2 and s3 - these are the
projections of this point onto the three coordinate axes.
The polarization ellipse parameter azimuth (Θ) angle is represented on the Poincare sphere as
the longitude = 2Θ, the ellipticity (h) angle appears as the latitude = 2h. Please note the factor
of 2 involved in the mapping - the figure below illustrates that.
The handedness defines the position on the northern (right handed rotation) or southern (left
handed rotation) hemisphere.
The equatorial plane (shown in red) represents all linear states of polarization.
The north pole represents right-turning circular polarization, the south pole - left-turning circular
polarization.
All other points on the northern and southern hemisphere correspond to elliptical states of po-
larization with correspondingly right and left handed rotation. Below are given some typical
states of polarization, and their azimuth and ellipticity values:
Changes of the state of polarization as a function of time can be displayed as a trace on the
Poincaré sphere.
To Next Page
Loading...
Need help?
General
