© 2019 Thorlabs GmbH
8 Tutorial
76
α is the radius in degrees. The factor ½ is due to the fact that azimuth and ellipticity are
mapped with a factor ½. The domain for azimuth is -90° to 90° (180° area). A circle has a range
of 360°.
In our measurement example this yields:
The center ellipticity is -0.95°. That means even if the circle would have a radius = 0, an ellipti-
city remains. This center ellipticity corresponds to
Both the radius and the center ellipticity have to be considered. The maximum ellipticity corres-
ponds to α/2 + | center ellipticity |:
This is the corrected for center ellipticity ER.
Correction for DOP (Degree of Polarization)
A polarimeter's ER measurement must also be corrected for DOP, as the unpolarized part of
the light is not considered. In other words, while the DOP does not affect the ER measurement
made by a polarimeter, the DOP may actually have a strong impact on the ER. This is espe-
cially true of the ER for linearly polarized light.
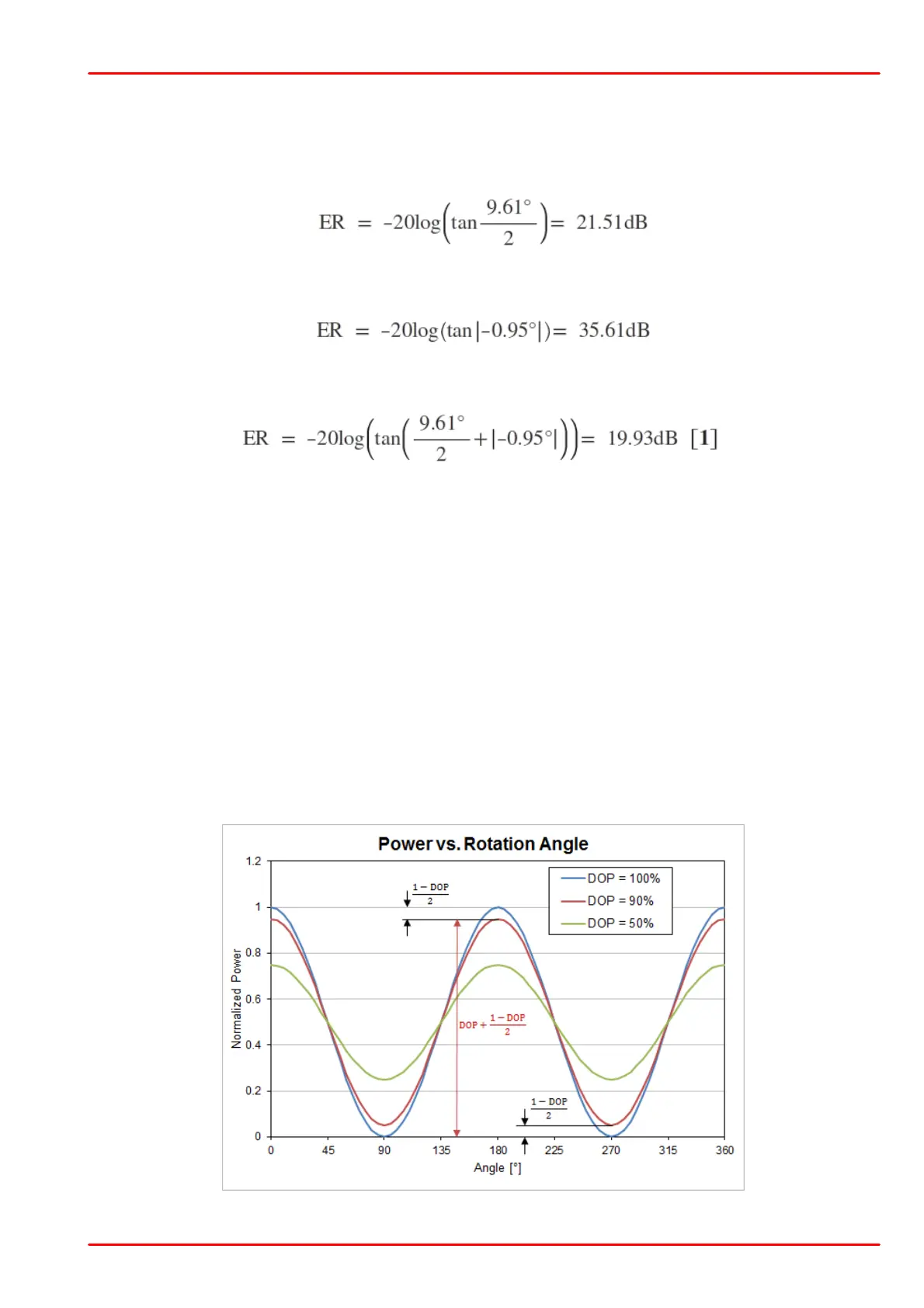
The spinning analyzer method, which is used by Thorlabs' ERM100, takes DOP into account
and accurately measures ER. As an example of how the DOP affects the ER, consider the fol-
lowing plot.
If the input light is linearly polarized, the measured photocurrent which is equivalent to the op-
tical power, shows two maxima and two minima per revolution of the polarizer.
If the light is 100% polarized, the maximum normalized power will be 1, and the minimum will
be 0. If the light is only partially polarized the maximum will shrink and an offset will be added.
The following diagram illustrates that:
Impact of the DOP on the ER Result (Spinning Analyzer Method)
To Next Page
Loading...
Need help?
General
