YOKOGAWA WT310EH - AC RLC Circuits

App-12
IM WT310E-01EN
AC RLC Circuits
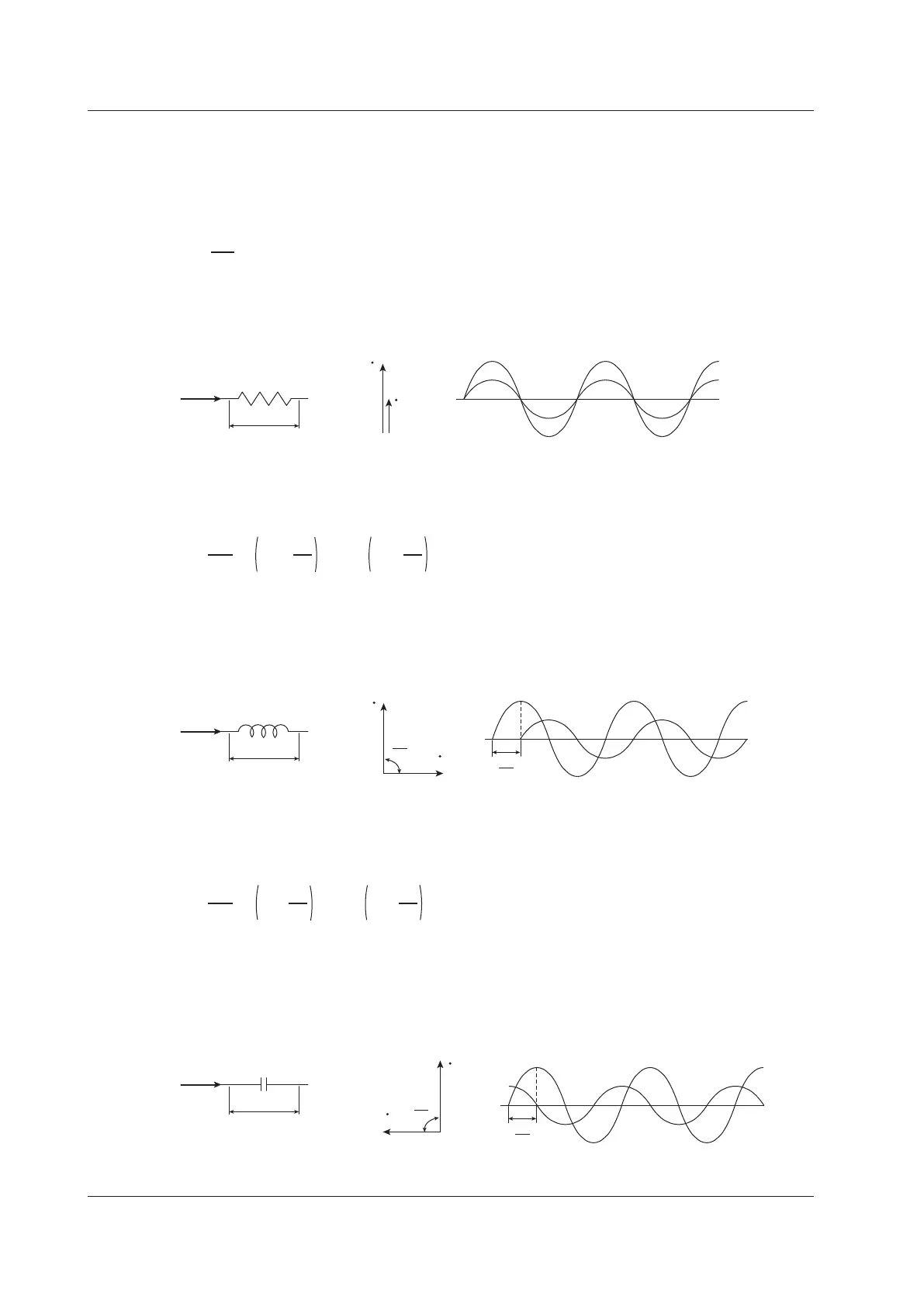
Resistance
ThecurrentiwhenanACvoltagewhoseinstantaneousvalueu=Umsinωtisappliedtoload
resistanceR[Ω]isexpressedbytheequationbelow.I
m
denotes the maximum current.
i =
U
m
R
sin
ωt
= I
msinωt
Expressedusingrmsvalues,theequationisI=U/R.
There is no phase difference between the current flowing through a resistive circuit and the voltage.
R
I
U
U
I
i
u
Inductance
ThecurrentiwhenanACvoltagewhoseinstantaneousvalueu=Umsinωtisappliedtoacoilloadof
inductanceL[H]isexpressedbytheequationbelow.
i =
Um
XL
sin ωt – sin ωt –
π
2
= I
m
π
2
Expressedusingrmsvalues,theequationisI=U/X
L
. X
L
is called inductive reactance and is defined
as X
L
=ωL.TheunitofinductivereactanceisΩ.
Inductance works to counter current changes (increase or decrease), and causes the current to lag the
voltage.
L
I
U
U
I
π
2
i
u
π
2
Capacitance
ThecurrentiwhenanACvoltagewhoseinstantaneousvalueu=UmsinωtisappliedtocapacitanceC
[F]isexpressedbytheequationbelow.
i =
U
m
XC
sin ωt + sin ωt +
π
2
= I
m
π
2
Expressedusingrmsvalues,theequationisI=U/X
C
. X
C
is called capacitive reactance and is defined
as X
C
=1/ωC.TheunitofcapacitivereactanceisΩ.
When the polarity of the voltage changes, the largest charging current with the same polarity as the
voltage flows through the capacitor. When the voltage decreases, discharge current with the opposite
polarity of the voltage flows. Thus, the current phase leads the voltage.
C
I
U
U
I
π
2
i
u
π
2
Appendix 2 Power Basics (Power, harmonics, and AC RLC circuits)