YOKOGAWA WT310EH User Manual

App-6
IM WT310E-01EN
Appendix 2 Power Basics (Power, harmonics, and
AC RLC circuits)
Thissectionexplainsthebasicsofpower,harmonics,andACRLCcircuits.
Power
Electrical energy can be converted into other forms of energy and used. For example, it can be
converted into the heat in an electric heater, the torque in a motor, or the light in a fluorescent or
mercury lamp. In these kinds of examples, the work that electricity performs in a given period of time (or
the electrical energy expended) is referred to as electric power. The unit of electric power is watts (W).
1wattisequivalentto1jouleofworkperformedin1second.
DC Power
The DC power P (in watts) is determined by multiplying the applied voltage U (in volts) by the current I (in
amps).
 P=UI[W]
In the example below, the amount of electrical energy determined by the equation above is retrieved
fromthepowersupplyandconsumedbyresistanceR(inohms)everysecond.
R
I
U
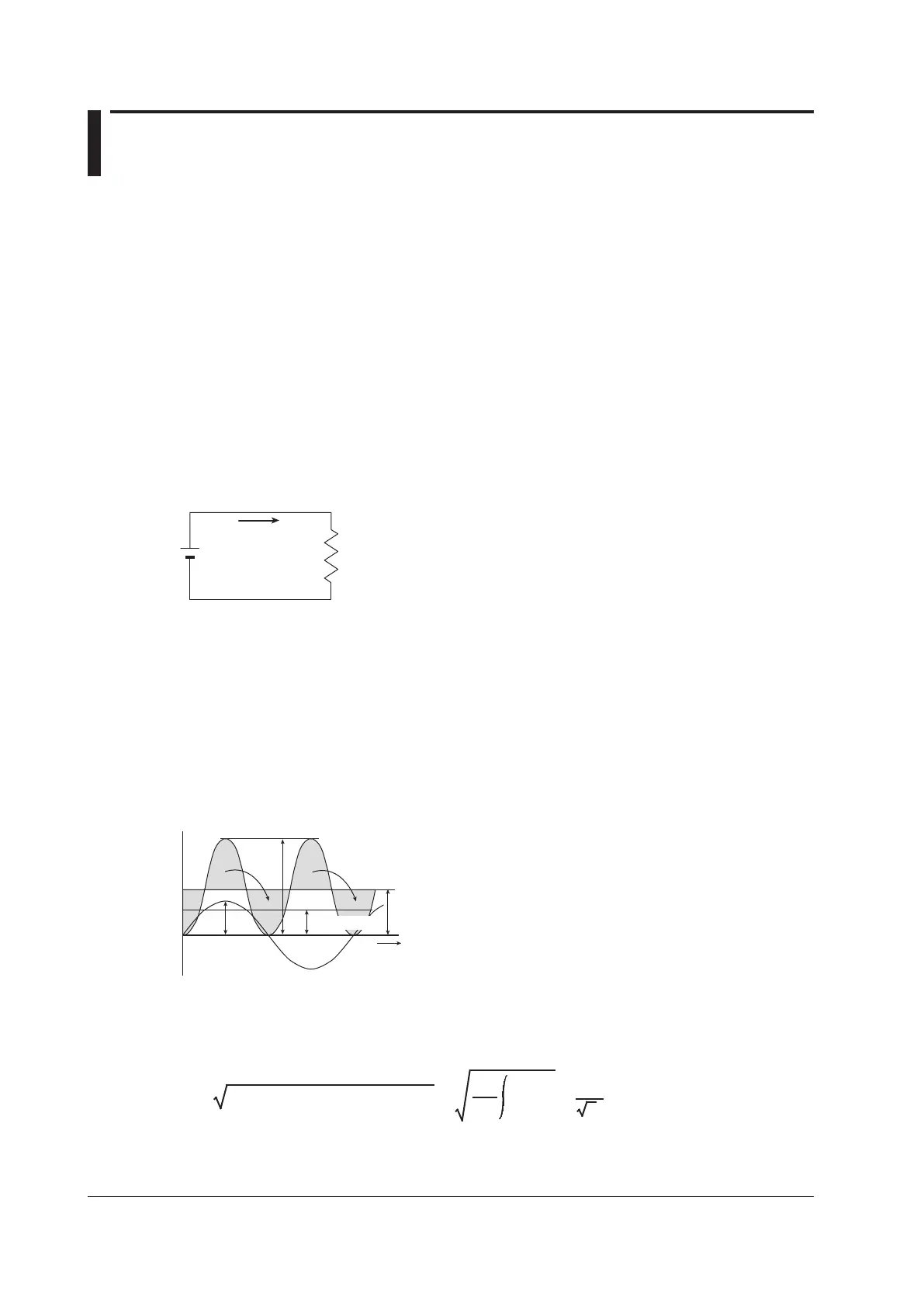
Alternating Current
Normally, the power supplied by power companies is alternating current with sinusoidal waveforms.
The magnitude of alternating current can be expressed using values such as instantaneous, maximum,
rms, and mean values. Normally, it is expressed using rms values.
TheinstantaneousvalueiofasinusoidalalternatingcurrentisexpressedbyImsinωt(whereAmisthe
maximumvalueofthecurrent,ωistheangularvelocitydefinedasω=2πf,andfisthefrequencyof
the sinusoidal alternating current). The thermal action of this alternating current is proportional to i
2
,
and varies as shown in the figure below.*
* Thermal action is the phenomenon in which watt hour is converted to heat energy when a current
flows through a resistance.
π
2π
ω t
i = Imsinωt
i
2
Im
Im
2
Rms value I
Average of i
2
The areas are the same.
The rms value (effective value) is the DC value that generates the same thermal action as the
alternating current. With I as the DC value that produces the same thermal action as the alternating
current:
I= The mean of i
2
over one period = =
1
2π
0
2
π
i
2
dωt
Im
2
Becausethisvaluecorrespondstotherootmeansquareoftheinstantaneousvaluesover1period,
the effective value is normally denoted using the abbreviation “rms.”

YOKOGAWA WT310EH Specifications

General

Brand	YOKOGAWA
Model	WT310EH
Category	Measuring Instruments
Language	English