SIRIUS®
6.1.1.3 Filter Order
An ideal filter has full transmission in the pass band, complete attenuation in the stop band, and an abrupt transition
between the two bands. In practice an ideal filter is not possible and can only be approached to a certain degree.
The higher the filter order, the more the filter will approach the ideal filter; but this also means that the impulse
response will be longer and that the latency will increase.
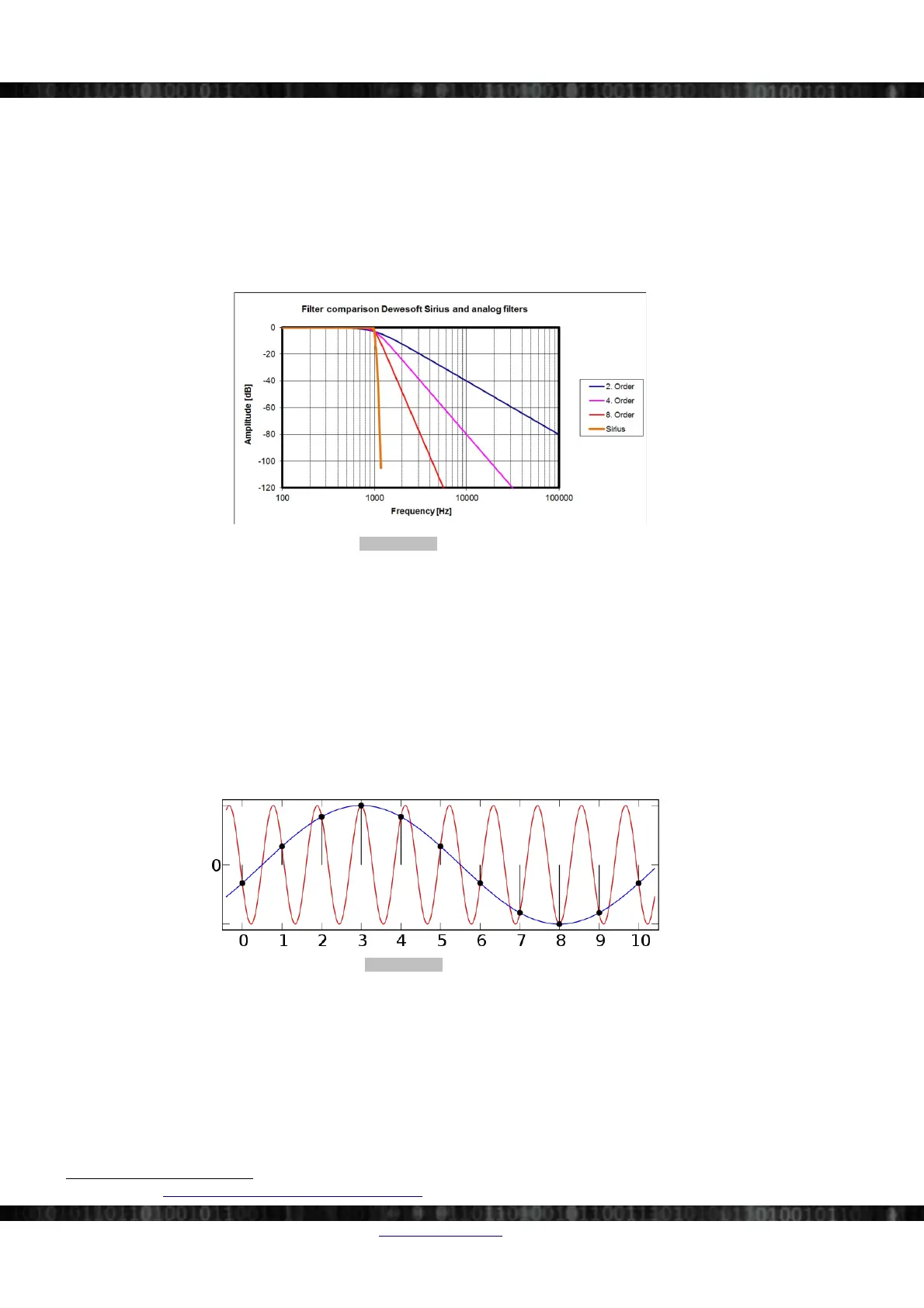
In Illustration 179 below you can see 3 analogue filters (2
nd
, 4
th
and 8
th
order) and the Sirius® filter (which is a
combination of analogue filter, oversampling and digital filter). Note, that filters with higher order have a sharper
damping around the filter frequency:
Illustration 179: Filter order
6.1.1.4 Aliasing
In signal processing, aliasing is an effect that causes different signals to become indistinguishable (or aliases of one
another) when sampled.
When signals are sampled (see also 8.2.1.1 Sampling on page 150), the sampling frequency must be at least twice as
high as the maximum frequency of the signal to avoid errors: this is called Nyquist theorem (Aliasing effect).
Illustration 180 below shows an example of aliasing. The red sine wave is the original signal, that we want to measure.
But our sampling frequency is too low (the sampling points are shown as black lollipops). When we now reconstruct the
sine wave by interpolating the sampled points, we get the blue signal, which is also a sine-wave, but has the wrong
frequency!
Illustration 180: Aliasing
23
Real world measurement signal are hardly ever pure sine waves and can thus have many components (harmonics) above
the Nyquist frequency. These harmonics are erroneously aliased back to the baseband and thus added to parts of the
accurately sampled signal which produces a distorted measurement signal. Filtering can be used to block frequencies
above the Nyquist bandwidth (which is half of the sample rate), to get correct measurement results.
23 Image Source: https://en.wikipedia.org/wiki/File:AliasingSines.svg
Page 128/166 www.dewesoft.com Doc-Version: 1.4.2

 Loading...
Loading...