168 Appendix A: Functions and Instructions
If you do not include any guesses and if any
equation is non-polynomial in any variable but all
equations are linear in all solution variables,
cSolve() uses Gaussian elimination to attempt to
determine all solutions.
cSolve(u_+v_=
e
^(w_) and u_ì v_=
i
, {u_,v_}) ¸
u_=
e
w_
2
+1/2ø
i
and v_=
e
w_
ì
i
2
If a system is neither polynomial in all of its
variables nor linear in its solution variables,
cSolve() determines at most one solution using
an approximate iterative method. To do so, the
number of solution variables must equal the
number of equations, and all other variables in
the equations must simplify to numbers.
cSolve(
e
^(z_)=w_ and w_=z_^2,
{w_,z_}) ¸
w_=.494… and z_=ë.703…
A non-real guess is often necessary to determine
a non-real solution. For convergence, a guess
might have to be rather close to a solution.
cSolve(
e
^(z_)=w_ and w_=z_^2,
{w_,z_=1+
i
}) ¸
w_=.149… + 4.891…ø
i
and
z_=1.588… + 1.540…ø
i
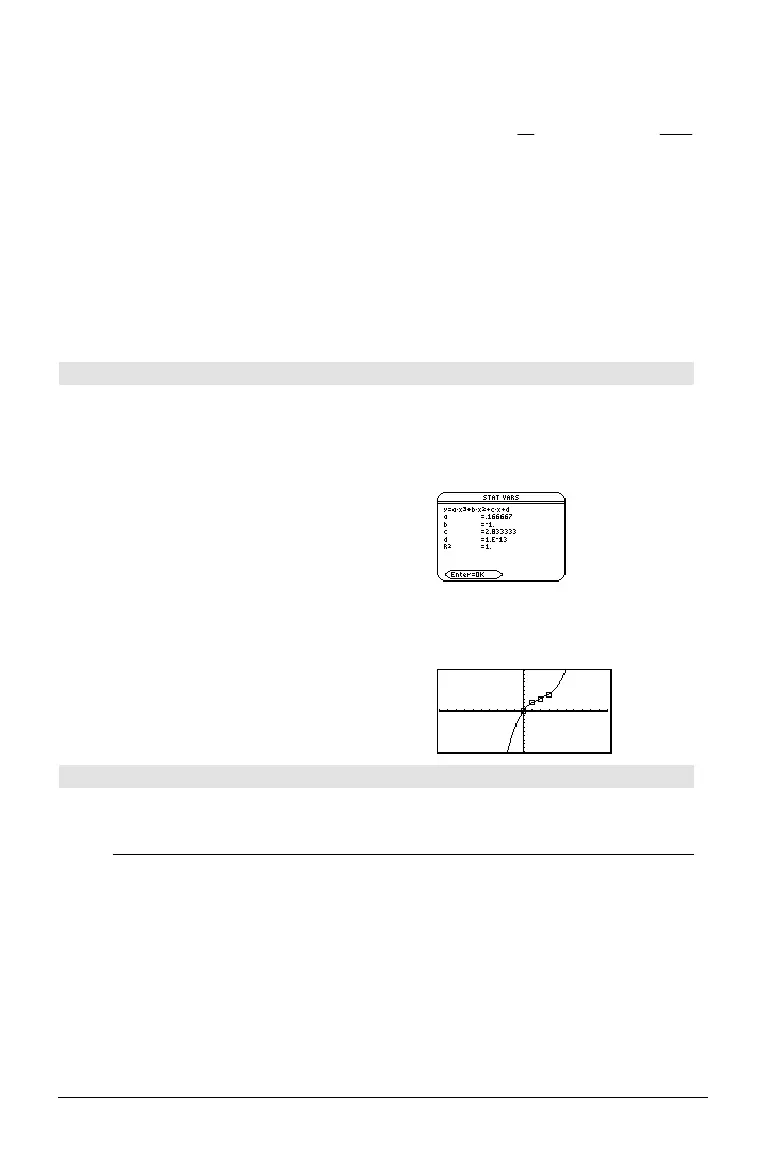
CubicReg MATH/Statistics/Regressions menu
CubicReg
list1
,
list2
[, [
list3
] [,
list4
,
list5
]]
Calculates the cubic polynomial regression and
updates all the statistics variables.
All the lists must have equal dimensions except
for
list5
.
list1
represents xlist.
list2
represents ylist.
list3
represents frequency.
list4
represents category codes.
list5
represents category include list.
Note:
list1
through
list4
must be a variable name
or c1–c99 (columns in the last data variable
shown in the Data/Matrix Editor).
list5
does not
have to be a variable name and cannot be c1–c99
.
In function graphing mode.
{0,1,2,3}! L1 ¸ {0 1 2 3}
{0,2,3,4}! L2
¸ {0 2 3 4}
CubicReg L1,L2
¸ Done
ShowStat
¸
¸
regeq(x)"y1(x)
¸ Done
NewPlot 1,1,L1,L2
¸ Done
¥%
cumSum() MATH/List menu
cumSum(
list1
) ⇒
list
Returns a list of the cumulative sums of the
elements in
list1
, starting at element 1.
cumSum({1,2,3,4}) ¸
{1 3 6 10}
cumSum(
matrix1
) ⇒
matrix
Returns a matrix of the cumulative sums of the
elements in
matrix1
. Each element is the
cumulative sum of the column from top to
bottom.
[1,2;3,4;5,6]! m1 ¸
1 2
3 4
5 6
cumSum(m1)
¸
1 2
4 6
9 12
To Next Page
Loading...
Need help?
General
