Thytronic Pro-N NVA100X-D

FUNCTION CHARACTERISTICS
49
NVA100X-D - Manual - 02 - 2016
Sequence
Fundamental RMS positive sequence current - side L: I
1
Fundamental RMS negative sequence current - side L: I
2
Fundamental RMS positive sequence voltage: U
1
Fundamental RMS negative sequence voltage: U
2
Demand
Fixed demand (I
L1FIX
, I
L2FIX
, I
L3FIX
, ±P
FIX
, ±Q
FIX
)
Inside an adjustable time interval t
FIX
, an average magnitude is calculated for phase currents I
L1
,
I
L2
, I
L3
, active power ±P and reactive power ±Q of measures taken every second. The average val-
ues are stored at the end of the same time interval.
Rolling demand (I
L1ROL
, I
L2ROL
, I
L3ROL
, ±P
ROL
, ±Q
ROL
)
Inside an adjustable time interval N
ROL
∙t
ROL
, an average magnitude is calculated for phase cur-
rents I
L1
, I
L2
, I
L3
, active power ±P and reactive power ±Q of measures taken every second, where
t
ROL
is the length of any time subinterval and N
ROL
is the number of the time intervals. The average
values are stored at the end of the same time subinterval.
Peak (I
L1MAX
, I
L2MAX
, I
L3MAX
, ±P
MAX
, ±Q
MAX
)
Inside an adjustable time interval t
ROL
, the maximum magnitude is calculated for phase currents
I
L1
, I
L2
, I
L3
, active power ±P and reactive power ±Q of measures taken every second. The average
values are stored at the end of the same time interval t
ROL
(Rolling demand common parameter).
•
•
•
•
•
•
•
I1-I2.ai
I
L1L
I
1
, I
2
I
2
= (I
L1
+ e
-j120°
I
L2
+ e
+j120°
I
L3
) / 3
I
1
= (I
L1
+ e
+j120°
I
L2
+ e
-j120°
I
L3
) / 3
I
L3
L
I
L2L
(I
n
)
e
-j120°
= -
√3
j
1
22
-
e
+j120°
= -
√3
j
1
22
+
I1-I2.ai
I
L1L
I
1
, I
2
I
2
= (I
L1
+ e
-j120°
I
L2
+ e
+j120°
I
L3
) / 3
I
1
= (I
L1
+ e
+j120°
I
L2
+ e
-j120°
I
L3
) / 3
I
L3
L
I
L2L
(I
n
)
e
-j120°
= -
√3
j
1
22
-
e
+j120°
= -
√3
j
1
22
+
U2.ai
U
L1
U
1
, U
2
U
2
= (U
L1
+ e
-j120°
U
L2
+ e
+j120°
U
L3
) / 3
U
1
= (U
L1
+ e
+j120°
U
L2
+ e
-j120°
U
L3
) / 3
U
L3
U
L2
e
-j120°
= -
√3
j
1
22
-
e
+j120°
= -
√3
j
1
22
+
(u
n
)
U2.ai
U
L1
U
1
, U
2
U
2
= (U
L1
+ e
-j120°
U
L2
+ e
+j120°
U
L3
) / 3
U
1
= (U
L1
+ e
+j120°
U
L2
+ e
-j120°
U
L3
) / 3
U
L3
U
L2
e
-j120°
= -
√3
j
1
22
-
e
+j120°
= -
√3
j
1
22
+
(u
n
)
Fix-Demand.ai
1s
I
L1FIX
, I
L2FIX
,I
L3FIX
±P
FIX
t
FIX
±P
±Q
(I
n
)
(P
n
)
(Q
n
)
±Q
FIX
I
L2L
I
L1L
I
L3L
I
LxFIX
I
Lxn
t
FIX
∙ 60
t
FIX
∙ 60
n=1
¥
1
±Q
FIX
= ±Q
n
t
FIX
∙ 60
t
FIX
∙ 60
n=1
¥
1
±P
FIX
= ±P
n
t
FIX
∙ 60
t
FIX
∙ 60
n=1
¥
1
t
FIX
t
FIX
t
FIX
Fix-Demand.ai
1s
I
L1FIX
, I
L2FIX
,I
L3FIX
±P
FIX
t
FIX
±P
±Q
(I
n
)
(P
n
)
(Q
n
)
±Q
FIX
I
L2L
I
L1L
I
L3L
I
LxFIX
I
Lxn
t
FIX
∙ 60
t
FIX
∙ 60
n=1
¥
1
±Q
FIX
= ±Q
n
t
FIX
∙ 60
t
FIX
∙ 60
n=1
¥
1
±P
FIX
= ±P
n
t
FIX
∙ 60
t
FIX
∙ 60
n=1
¥
1
t
FIX
t
FIX
t
FIX
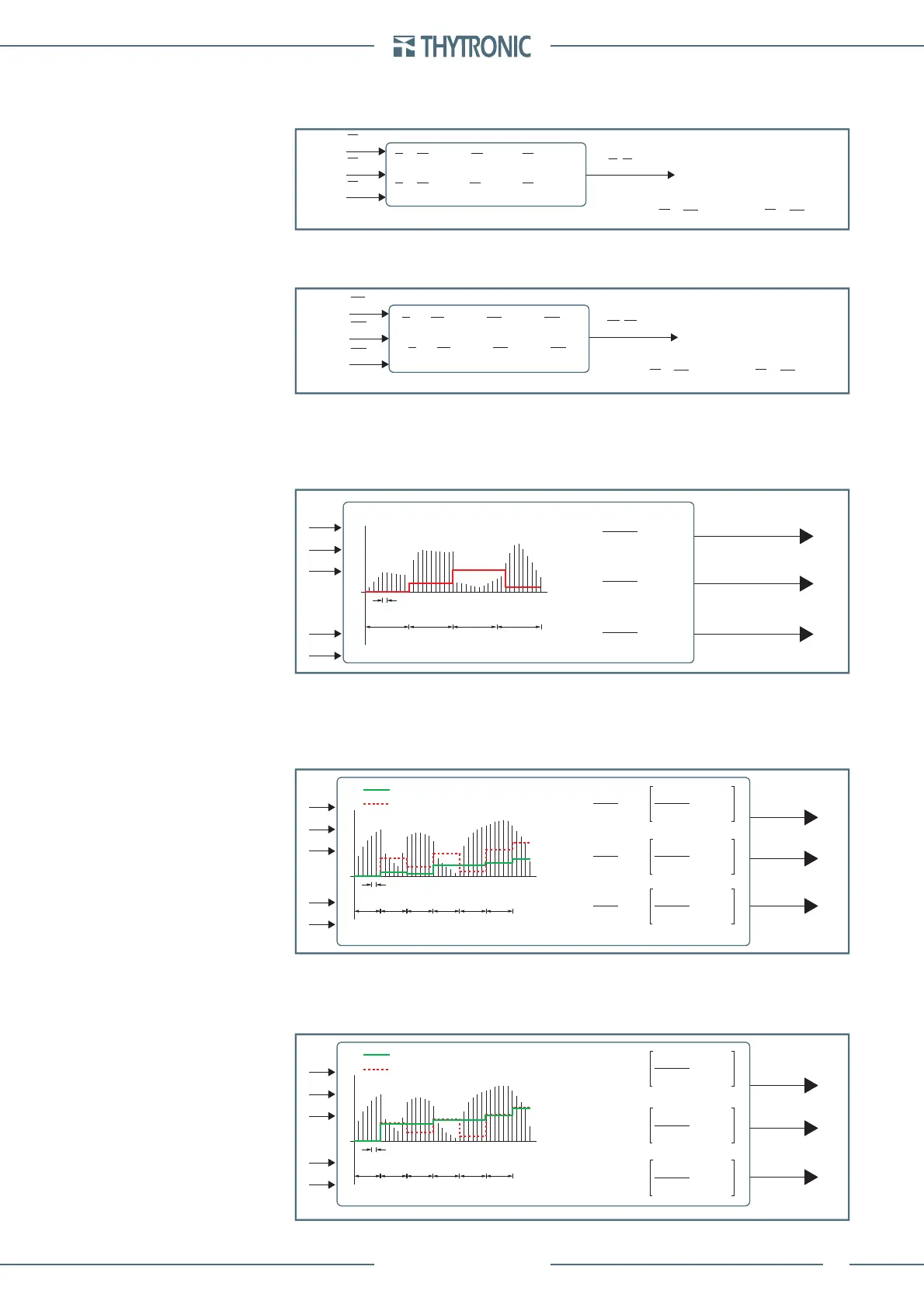
Rol-Demand.ai
Rolling demand example with
N
ROL
=4
I
L1ROL
I
L2ROL
I
L3ROL
±P
ROL
±P
±Q
(I
n
)
(P
n
)
(Q
n
)
±Q
ROL
I
L2L
I
L1L
I
L3L
012345
1s
t
ROL
t
ROL
N
ROL
t
ROL
t
ROL
t
ROL
6
t
ROL
I
LxROL
= I
Lxk
t
ROL
∙60
t
ROL
∙60
k=1
¥
N
ROL
n=1 n
¥
1
N
ROL
1
±P
ROL
=±P
k
t
ROL
∙60
t
ROL
∙60
k=1
¥
N
ROL
n=1 n
¥
1
N
ROL
1
±Q
ROL
=±Q
k
t
ROL
∙60
t
ROL
∙60
k=1
¥
N
ROL
n=1 n
¥
1
N
ROL
1
Average inside time interval t
ROL
Rol-Demand.ai
Rolling demand example with N
ROL
=4
I
L1ROL
I
L2ROL
I
L3ROL
±P
ROL
±P
±Q
(I
n
)
(P
n
)
(Q
n
)
±Q
ROL
I
L2L
I
L1L
I
L3L
012345
1s
t
ROL
t
ROL
N
ROL
t
ROL
t
ROL
t
ROL
6
t
ROL
I
LxROL
= I
Lxk
t
ROL
∙60
t
ROL
∙60
k=1
¥
N
ROL
n=1 n
¥
1
N
ROL
1
±P
ROL
=±P
k
t
ROL
∙60
t
ROL
∙60
k=1
¥
N
ROL
n=1 n
¥
1
N
ROL
1
±Q
ROL
=±Q
k
t
ROL
∙60
t
ROL
∙60
k=1
¥
N
ROL
n=1 n
¥
1
N
ROL
1
Average inside time interval t
ROL
Maximum value of averages inside time interval t
ROL
Average inside time interval
t
ROL
Max-Demand.ai
I
L1MAX
I
L2MAX
I
L3MAX
±P
MAX
±P
±Q
(I
n
)
(P
n
)
(Q
n
)
±Q
MAX
I
L2L
I
L1L
I
L3L
1s
t
ROL
t
ROL
t
ROL
t
ROL
t
ROL
t
ROL
MAX
I
LxMAX
= I
Lxn
t
ROL
∙60
t
ROL
∙60
n=1
¥
1
MAX
±P
MAX
=±P
n
t
ROL
∙60
t
ROL
∙60
n=1
¥
1
MAX
±Q
MAX
=±Q
n
t
ROL
∙60
t
ROL
∙60
n=1
¥
1
Maximum value of averages inside time interval t
ROL
Average inside time interval
t
ROL
Max-Demand.ai
I
L1MAX
I
L2MAX
I
L3MAX
±P
MAX
±P
±Q
(I
n
)
(P
n
)
(Q
n
)
±Q
MAX
I
L2L
I
L1L
I
L3L
1s
t
ROL
t
ROL
t
ROL
t
ROL
t
ROL
t
ROL
MAX
I
LxMAX
= I
Lxn
t
ROL
∙60
t
ROL
∙60
n=1
¥
1
MAX
±P
MAX
=±P
n
t
ROL
∙60
t
ROL
∙60
n=1
¥
1
MAX
±Q
MAX
=±Q
n
t
ROL
∙60
t
ROL
∙60
n=1
¥
1