HP 33S Owner's Manual

Operations with Complex Numbers
9–5
File name 33s-E-Manual-1008-Publication(1st).doc Page : 386
Printed Date : 2003/10/8 Size : 13.7 x 21.2 cm
Evaluate
2−
z
e
, where z = (1 + i ). Use
¹ c )
to evaluate z
–2
;
enter –2 as –2 + i 0.
Keys: Display: Description:
1
Ï
1
Ï
0
Ï
2
z ¹
c
)



Intermediate result of
(1 + i )
–2
¹ c #


Real part of final results.
Final result is
0.8776 – i 0.4794.
Using Complex Numbers in Polar Notation
Many applications use real numbers in polar form or polar notation. These forms
use pairs of numbers, as do complex numbers, so you can do arithmetic with these
numbers by using the complex operations. Since the HP 33s's complex operations
work on numbers in rectangular form, convert polar form to rectangular form
(using
º ±
) before executing the complex operation, then convert the
result back to polar form.
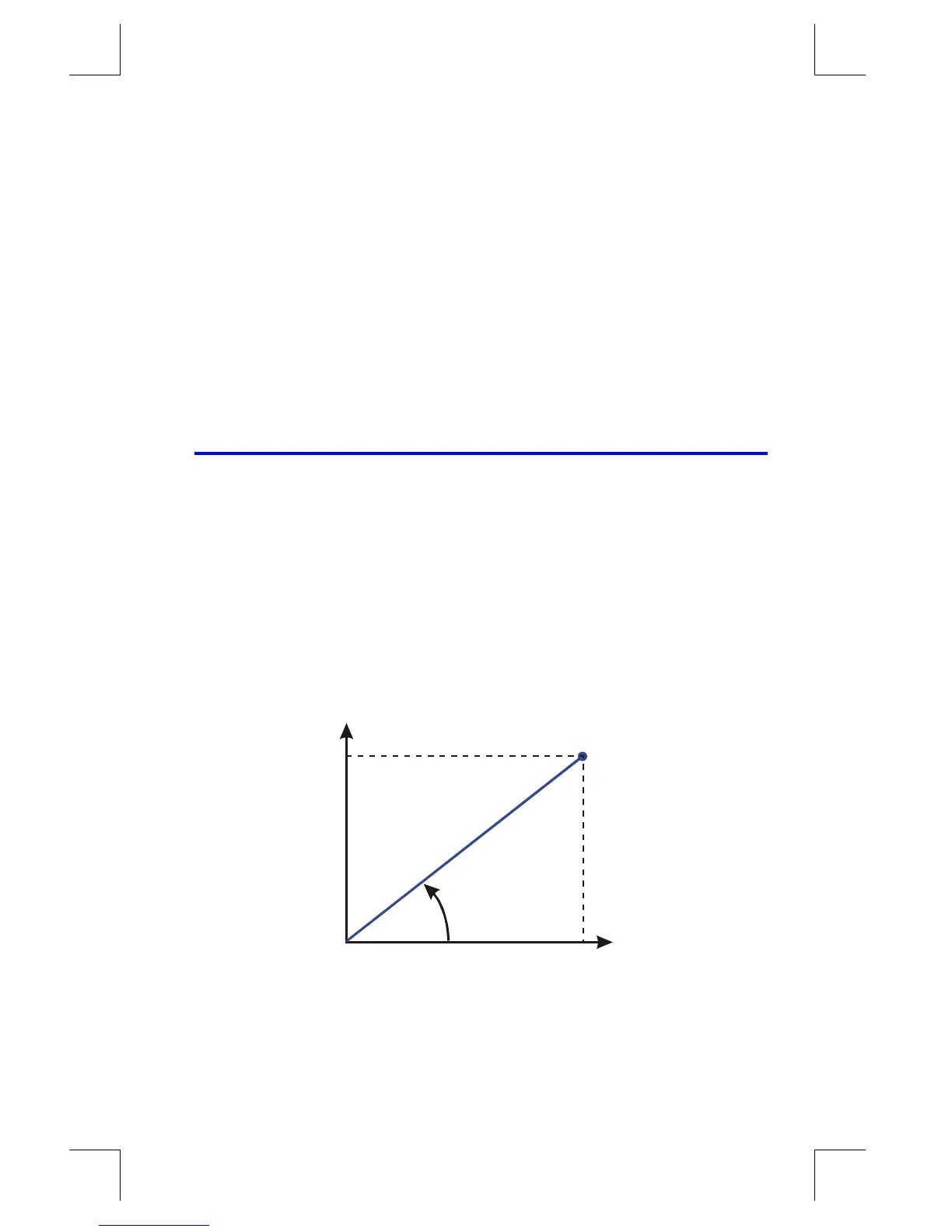
a + i b = r (cos
θ
+ i sin
θ
) = re
iθ
= r
∠
θ
(Polar or phase form)
r
real
(a, b)
imaginary
θ
Example: Vector Addition.
Add the following three loads. You will first need to convert the polar coordinates
to rectangular coordinates.


HP 33S Specifications

General

Type	Scientific
Form factor	Pocket
Product color	Silver
Digits	10 digits
Display number of lines	2 lines
Keyboard type	Alphanumeric
Menus and prompts	Yes

Weight and Dimensions

Dimensions (WxDxH)	157 x 16 x 81 mm