Chapter 6 ______________________________________________________ Processing Algorithms
VAISALA______________________________________________________________________ 201
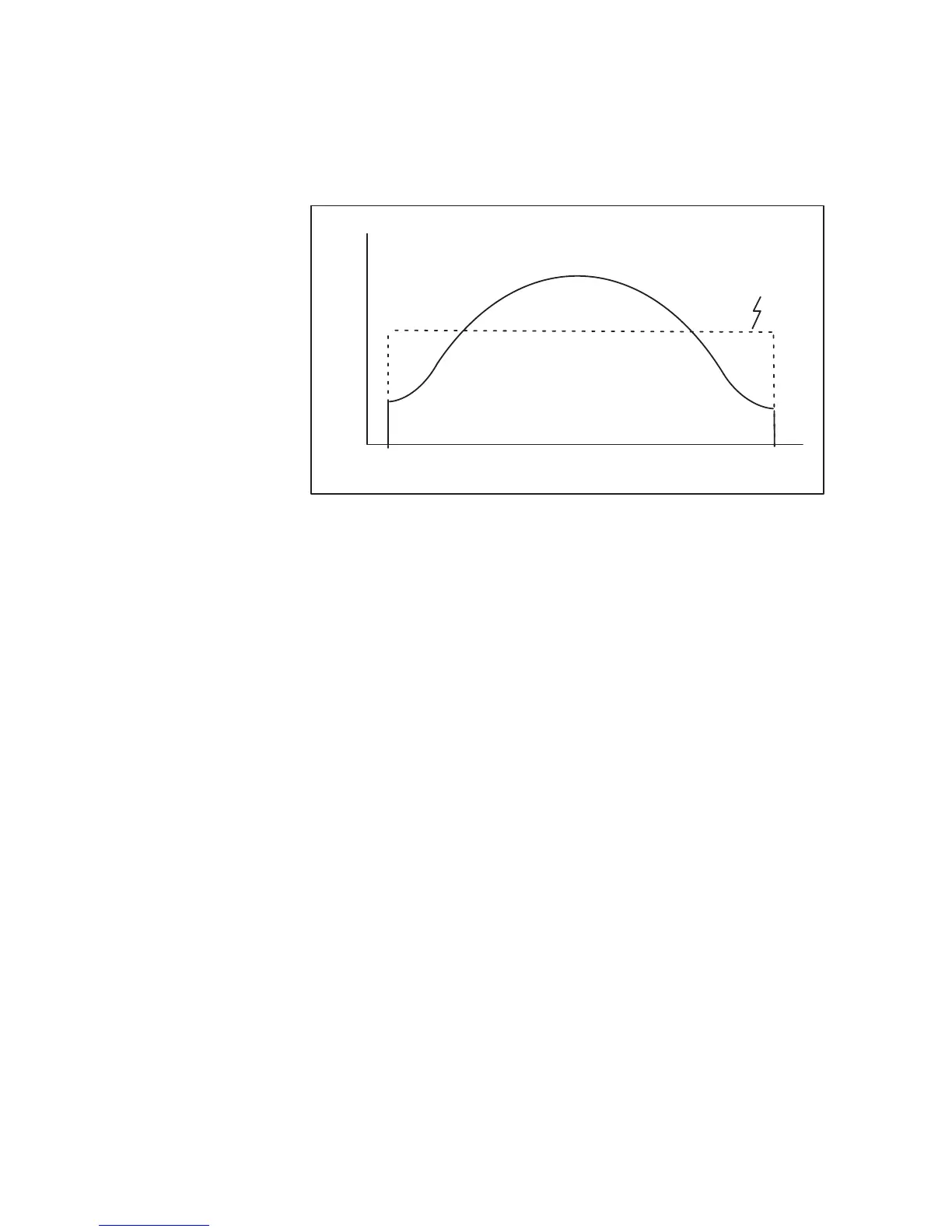
the rectangular window. The "gain" of the window is set to preserve the
total power.
0916-053
Figure 39 Typical Form of Time Series Window
Even though the window gain can be adjusted to conserve the total power,
there is an effective reduction in the number of samples which increases
the variance (or uncertainty) of the moment estimates. For example the
variance of the total power is greater when computed from a spectrum with
Blackman weighting as compared to using a rectangular window. This is
because there are effectively fewer samples because of the de-emphasis of
the end points. This is a negative side to using a window.
The DFT of the window itself is known as its impulse response which
shows all of the frequencies that are generated by the window itself. A
generic example is shown in Figure 40 on page 200 below which illustrates
that these "side lobe" frequencies can have substantial power. This is not a
problem for weather signals alone, but if there is strong clutter mixed in,
then the side lobe power from the clutter can obscure the weaker weather
signals. The rectangular window has the worst sidelobes, but the narrowest
window width. However, the rectangular window provides the lowest
variance estimates of the moment parameters (in the absence of clutter.
More "aggressive" windows have lower side lobe power at the expense of
a broader impulse response and an increased variance of the moment
estimates.

 Loading...
Loading...