2-401
2 Instruction Descriptions
NJ-series Instructions Reference Manual (W502)
Conversion Instructions
2
PIDAT
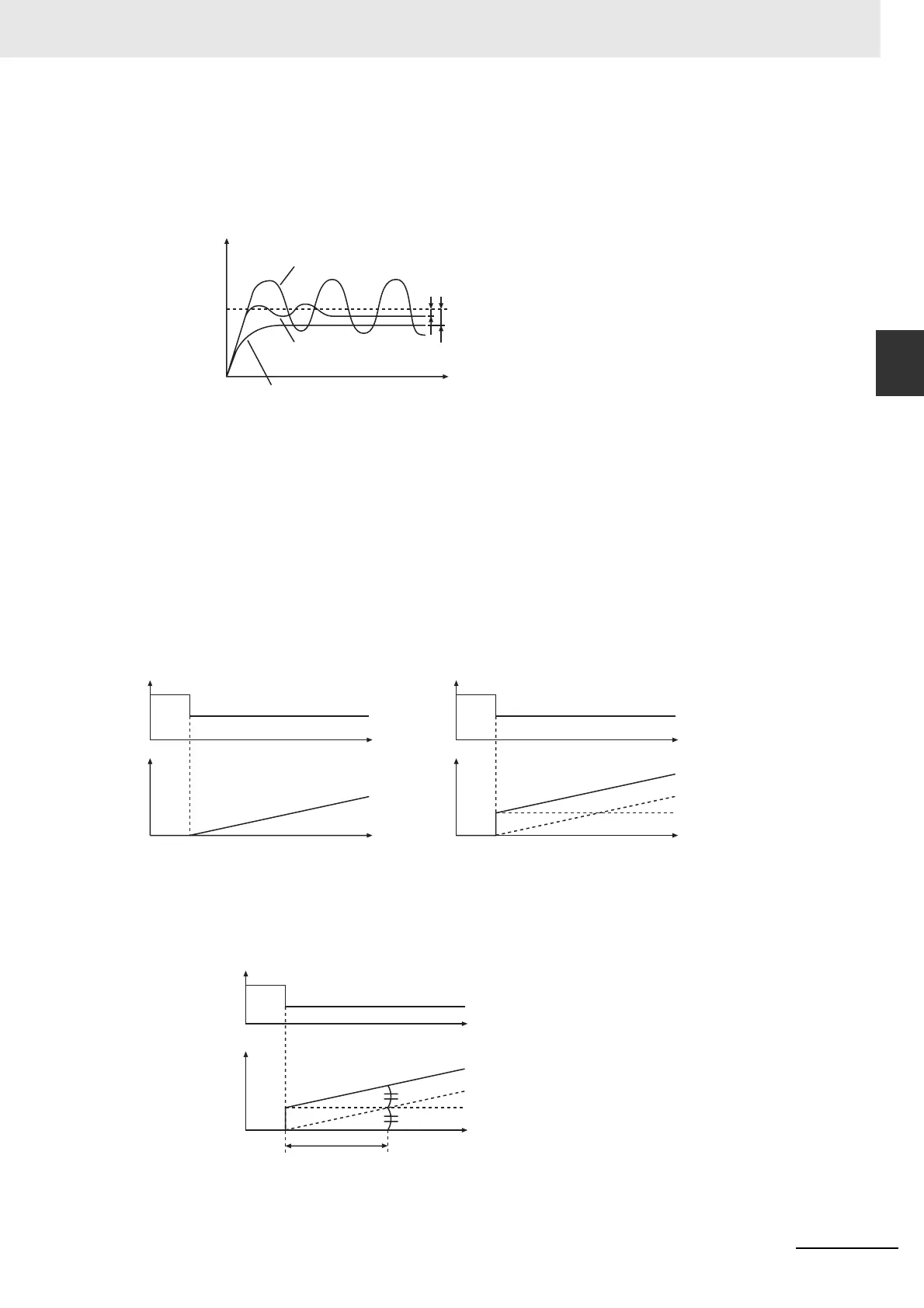
If the manual reset value is not suitable, the deviation will never reach 0. The remaining deviation is
called the offset or the residual deviation. You can make the proportional band narrower to reduce
the offset. If the proportional band is too narrow, the process value will not stop at the set point. This
is called overshooting. If the process value does not stabilize and oscillates around the set point, it is
called hunting.
z Integral Action (I)
Very accurate adjustment of the proportional band and manual reset value is required to bring the
offset to 0 with only the proportional action. Also, the size of the offset varies with the disturbance, so
it is necessary to repeat the adjustment frequently. To simplify the operation, an integral action is
used in combination with the proportional action. The integral action integrates the deviation on the
time axis and then increases the absolute value of the manipulated variable in proportion to the
result. When normal distribution operation is performed, the manual reset value is ignored. The fol-
lowing graph on the left shows changes in the manipulated variable for the integral action when a
deviation occurs in stepwise fashion. The following graph on the right shows changes in the manipu-
lated variable when the integral and proportional actions are combined.
One of the parameters for the integral action is the integration time. This is the time for the manipu-
lated variable from the integral action to equal the manipulated variable from the proportional action
when a stepwise deviation occurs. The shorter the integration time is, the stronger the integral action
is. A short integration time reduces the time for the offset to reach 0, but it can also cause hunting.
Proportional band is too narrow
(hunting occurs).
The proportional band is suitable.
Proportional band is too wide
(there is a large offset).
Offset
Time
Process value
Set point
Manipulated Variable for Integral Action
00
00
Stepwise response
Manipulated Variable for Integral and
Proportional Actions Together
Stepwise response
Time
Time
Deviation Deviation
Proportional and integral actions
Integral action only
Proportional action only
Time
Time
Manipulated
variable
Manipulated
variable
0
Stepwise response
Time
Deviation
0
Proportional and integral actions
Integral action only
Proportional action only
Time
Integration time
Manipulated
variable

 Loading...
Loading...