MAN B&W 2.02
Page 1 of 2
MAN Diesel
198 38 782.5MAN B&W MC/MC-C, ME/ME-GI/ME -B engines
D = Optimum propeller diameters
P/D = Pitch/diameter ratio
Shaft power
kW
8.500
8.600
8.700
8.800
8.900
9.000
9.100
9.200
9.300
9.400
9.500
70
80
90
100
110
120
130
r/min
Propeller
speed
P/D
1.00
0.95
0.90
0.85
0.80
D
7.4m
0.75
7.2m
7.0m
6.8m
6.6m
0.70
0.65
0.60
0.55
D
P/D
0.50
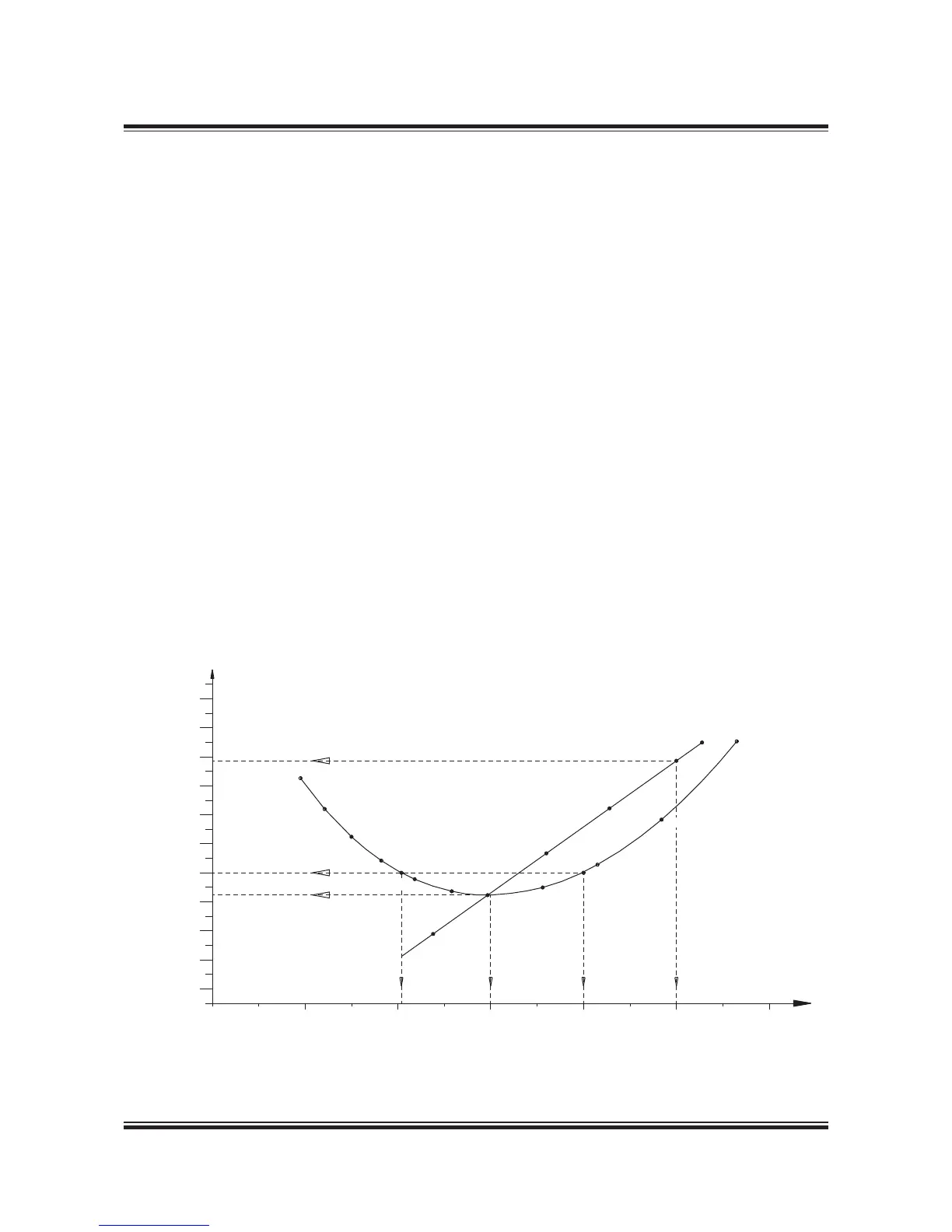
Fig. 2.02.01: Influence of diameter and pitch on propeller design
Propeller diameter and pitch, influence on the optimum propeller speed
In general, the larger the propeller diameter D,
the lower is the optimum propeller speed and the
kW required for a certain design draught and ship
speed, see curve D in the figure below.
The maximum possible propeller diameter de-
pends on the given design draught of the ship,
and the clearance needed between the propeller
and the aft body hull and the keel.
The example shown in the figure is an 80,000 dwt
crude oil tanker with a design draught of 12.2 m
and a design speed of 14.5 knots.
When the optimum propeller diameter D is in-
creased from 6.6 m to 7.2. m, the power demand
is reduced from about 9,290 kW to 8,820 kW, and
the optimum propeller speed is reduced from 120
r/min to 100 r/min, corresponding to the constant
ship speed coefficient ∝ = 0.28 (see definition of
∝ in Section 2.02, page 2).
Once an optimum propeller diameter of maximum
7.2 m has been chosen, the corresponding op-
timum pitch in this point is given for the design
speed of 14.5 knots, i.e. P/D = 0.70.
However, if the optimum propeller speed of 100
r/min does not suit the preferred / selected main
engine speed, a change of pitch away from opti-
mum will only cause a relatively small extra power
demand, keeping the same maximum propeller
diameter:
• going from 100 to 110 r/min (P/D = 0.62) requires
8,900 kW i.e. an extra power demand of 80 kW.
• going from 100 to 91 r/min (P/D = 0.81) requires
8,900 kW i.e. an extra power demand of 80 kW.
In both cases the extra power demand is only
of 0.9%, and the corresponding ‘equal speed
curves’ are ∝ =+0.1 and ∝ =0.1, respectively, so
there is a certain interval of propeller speeds in
which the ‘power penalty’ is very limited.
178 47 032.0

 Loading...
Loading...