Bruker AVANCE NEO - Exclusion Zone; Security Zone; The Safety Lines

Introductory Theory and Terminology
10 / 86 H171804E_14_001
2) Local Atomic Environment:
Superimposed on the basic resonance frequency is an effect due to the local atomic
environment in which an isotope is situated. The precise value of the resonance frequency of
a
1
H nucleus in a particular compound will depend upon the atoms it is bonded to and
surrounded by. The nucleus is surrounded by electrons which may be viewed as moving
electrical charges with associated magnetic fields. These electrons act as a source of
magnetic shielding for the nucleus. The extent of the shielding will depend on the precise
local atomic environment. The size of typical local field variations (which will result in a
frequency variation) will depend on the isotope and the strength of the magnetic field in which
the sample is placed. The table below shows the typical frequency variation for two of the
most widely used NMR nuclei,
1
H and
13
C. It is clear that the local atomic environment has a
relatively small effect on the basic resonance frequency.
Nucleus Typical variation in basic resonance frequency due to
local atomic environment.
1
H 6 kHz
13
C 30 kHz
Table3.2: Frequency Variations (quoted for an 11.7 T magnet)
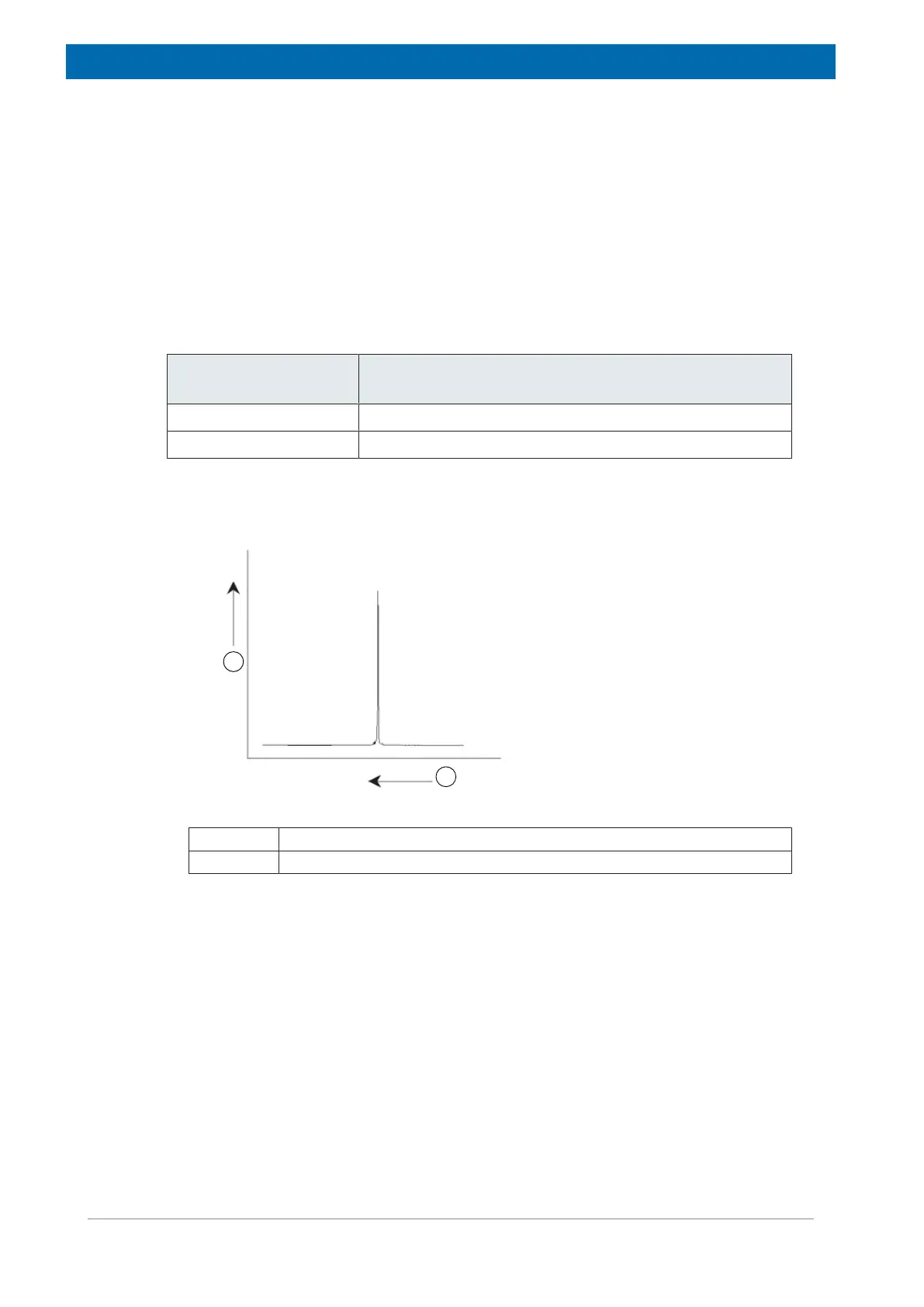
NMR signals are usually plotted as spectra and analyzed with respect to two features,
frequency and intensity. It is conventional in NMR to plot frequency on the horizontal axis
and increasing towards the left.
1
2
Figure3.2: NMR Spectrum
1. Intensity
2. Frequency
As mentioned above, the frequency yields qualitative information regarding the local atomic
environment. The integrated intensity of a signal is a measure of signal strength and is
determined by integrating the area under the signal peak. The integral will be directly
proportional to the number of nuclei contributing to a signal at a particular frequency (if all
nuclei are equally excited) and hence will provide quantitative information regarding chemical
structure.
To excite a given nucleus in an NMR experiment, the frequency of the excitation pulse should
closely match the resonance frequency of the nucleus. This frequency is referred to as the
carrier frequency. Thus, if experiments are carried out using a 11.7 T magnet, the
1
H nuclei
would require a carrier frequency of approximately 500 MHz, whereas
13
C nuclei would
require a carrier frequency close to 126 MHz. The carrier frequency is specified by the
parameter SFO1. The nucleus that is excited by this carrier frequency is referred to as the
observe nucleus.