6-35
6 Programming
NJ-series CPU Unit Software User’s Manual (W501)
6-3 Variables
6
6-3-5 Data Types
This floating-point format follows the IEEE 754 standard. The formats are given below.
Example: Expressing 86.625 as REAL Data
1
This is a negative number, so s =1.
2
86.625 in binary is 1010110.101.
3
Normalizing this value gives us 1.010110101 2
6
.
4
From the above expression we can determine that e127 = 6, so e = 133 (or 10000101 in
binary).
5
Next we take the value after the decimal part of 1.010110101, which is 010110101. This is not
enough for the 23-bit mantissa, so f is this number with the required amount of zeroes added to
the end. Therefore, f = 01011010100000000000000.
Therefore, you can express 86.625 as shown in the following figure.
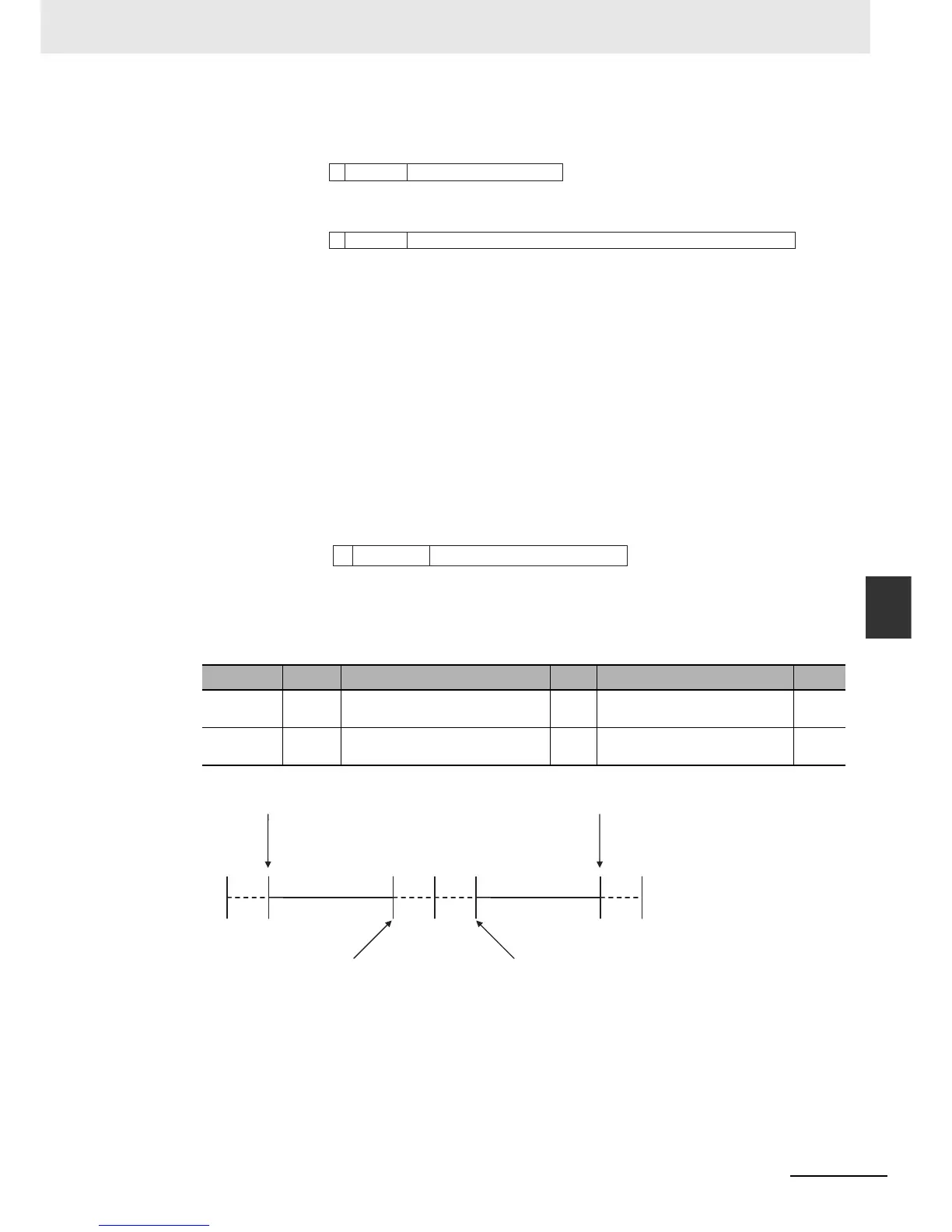
Valid Ranges
The valid ranges for REAL and LREAL data are shown in the following table. There are a range of
values that you cannot express as you approach 0.
Data type
Negative numbers 0 Positive numbers
REAL
3.402823e+38 to 1.175495e-38 0 +1.175495e38 to
+3.402823e+38
LREAL
1.79769313486231e+308 to
2.22507385850721e308
0 +2.22507385850721e308 to
+1.79769313486231e+308
s
31 30 23 22
0
ef
MantissaExponentSign
REAL data (32 bits)
s
63 62 52 51
0
ef
MantissaExponentSign
LREAL data (64 bits)
−∞ +∞
REAL −3.402823e+38
LREAL −1.79769313486231e+308
REAL +3.402823e+38
LREAL +1.79769313486231e+308
REAL −1.175495e−38
LREAL −2.22507385850721e−308
REAL +1.175495e−38
LREAL +2.22507385850721e−308
0
To Next Page
Loading...
Need help?
General
