FX Series Programmable Controlers Applied Instructions 5
5-129
Configuring the PID loop
The PID loop can be configured to offer variations on PID control. These are as follows:
It should be noted that in all situations there must be a proportional or ‘P’ element to the loop.
P - proportional change
When a proportional factor is applied, it calculates the difference between the Current Error
Value, EV
n
, and the Previous Error Value, EV
n-1
. The Proportional Change is based upon how
fast the Process Value is moving closer to (or further away from) the Set Point Value NOT
upon the actual difference between the PV
nf
and SV.
Note: Other PID systems might operate using an equation that calculates the Proportional
change based upon the size of the Current Error Value only.
I - integral change
Once a proportional change has been applied to an error situation, ‘fine tuning’ the correction
can be performed with the I or integral element.
Initially only a small change is applied but as time increases and the error is not corrected the
integral effect is increased. It is important to note how T
I
actually effects how fast the total
integral correction is applied. The smaller T
I
is, the bigger effect the integral will have.
Note: The T
I
value is set in data register S3+4. Setting zero for this variable disables the
Integral effect.
The Derivative Change
The derivative function supplements the effects caused by the proportional response. The
derivative effect is the result of a calculation involving elements T
D
,T
S
, and the calculated
error. This causes the derivative to initially output a large corrective action which dissipates
rapidly over time. The speed of this dissipation can be controlled by the value T
D
:Ifthevalue
of T
D
is small then the effect of applying derivative control is increased.
Because the initial effect of the derivative can be quite severe there is a ‘softening’ effect which
can be applied through the use of K
D, the derivative gain. The action of KD could be
considered as a filter allowing the derivative response to be scaled between 0 and 100%.
The phenomenon of chasing, or overcorrecting both too high and too low, is most often
associated with the Derivative portion of the equation because of the large initial correction
factor.
Note: The T
D
value is set in Data register S
3
+6. Setting zero for this variable disables the
Derivative effect.
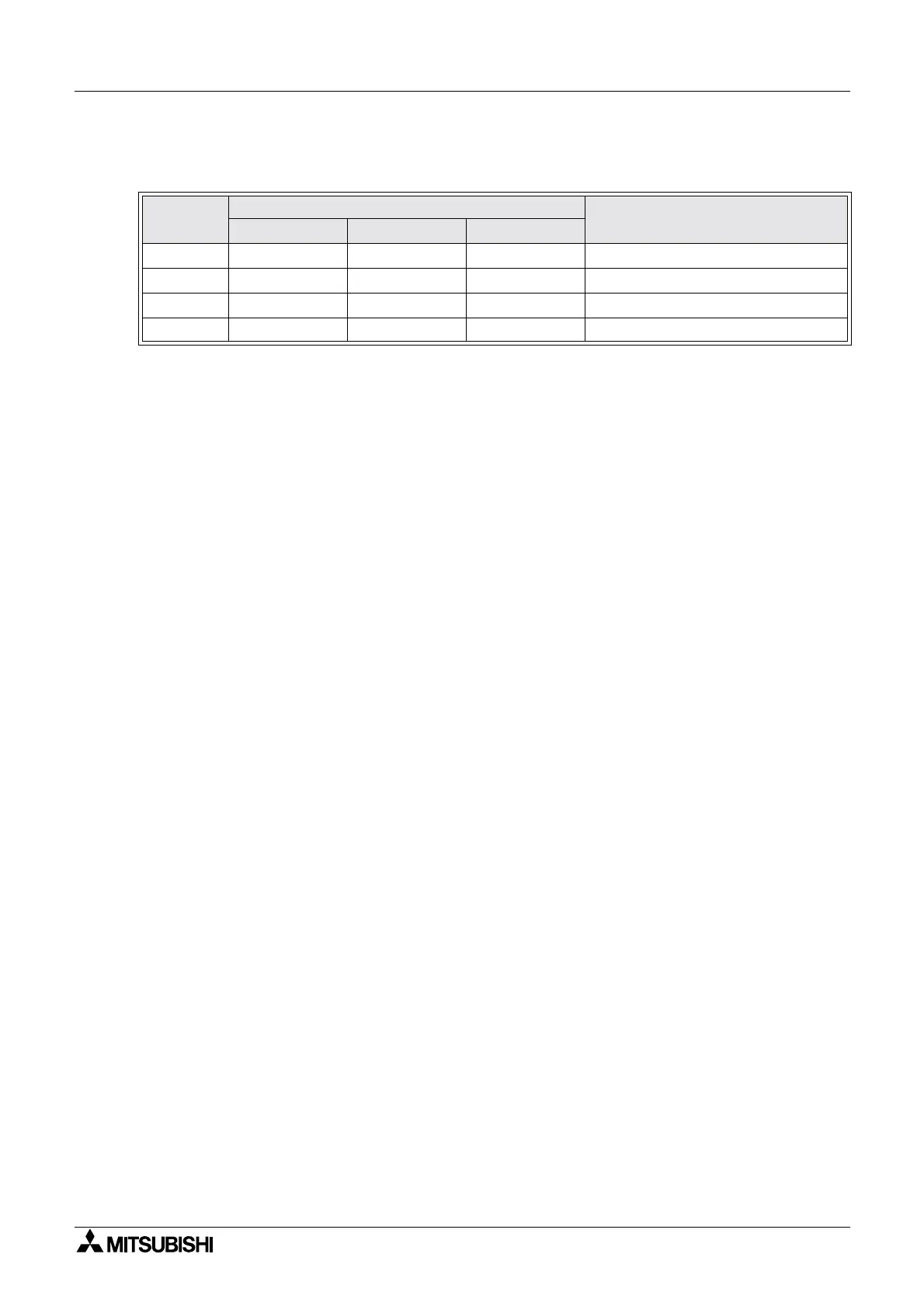
Control
method
Selection via setup registers
Description
S3 +3 (KP) S3+4(TI) S3 +6(TD)
P User value Set to 0 (zero) Set to 0 (zero) Proportional effect only
PI User value User value Set to 0 (zero) Proportional and integral effect
PD User value Set to 0 (zero) User value Proportional and derivative effect
PID User value User value User value Full PID

 Loading...
Loading...











