297
18-4 Calculating and Graphing Paired-Variable
Statistical Data
Under “Plotting a Scatter Diagram,” we displayed a scatter diagram and then per-
formed a logarithmic regression calculation. Let’s use the same procedure to look at
the six regression functions.
kk
kk
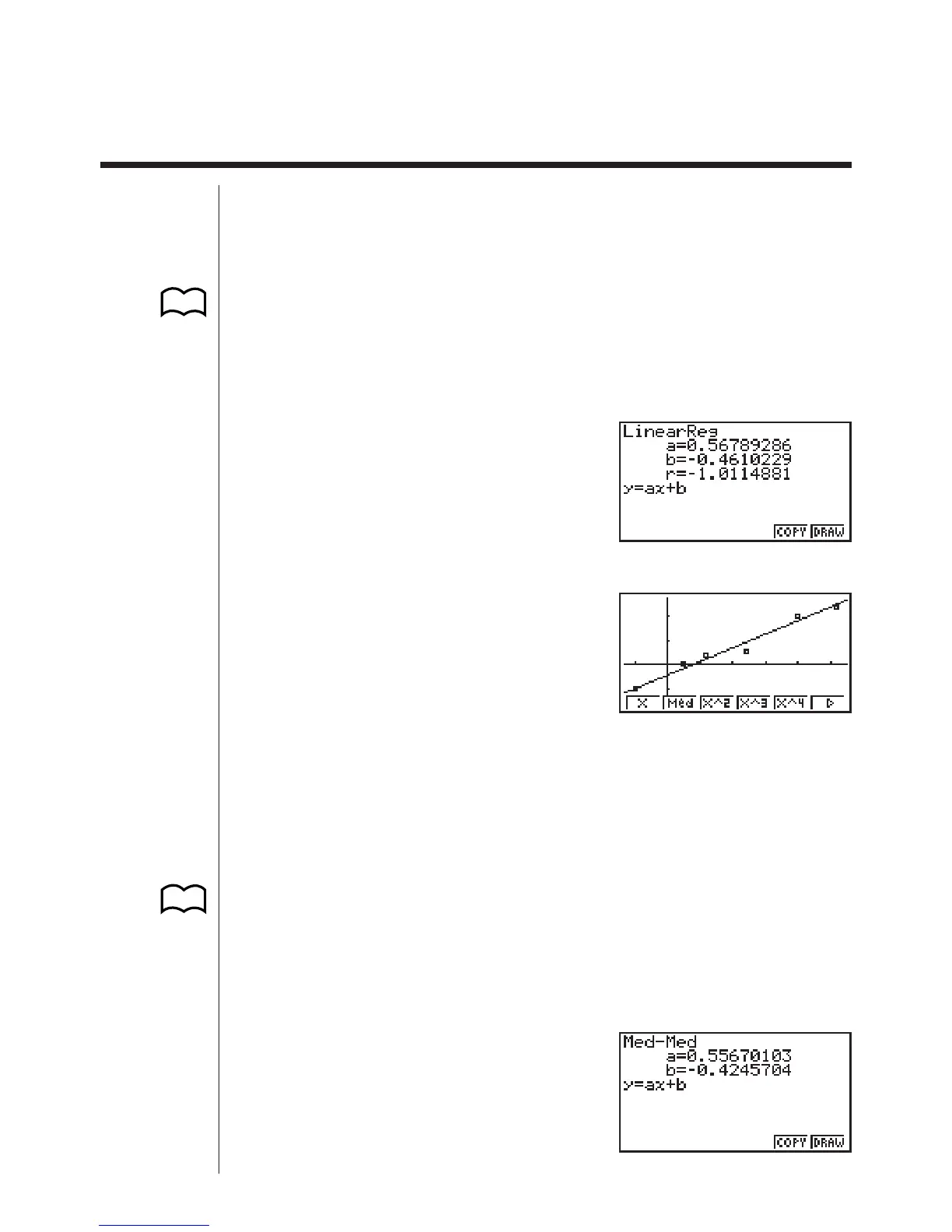
k Linear Regression Graph
Linear regression plots a straight line that passes close to as many data points as
possible, and returns values for the slope and y-intercept (y-coordinate when x = 0)
of the line.
The graphic representation of this relationship is a linear regression graph.
!Q1(GRPH)6(SET)c
1(Scat)
!Q1(GRPH)1(GPH1)
1(X)
6(DRAW)
The following are the meanings of the above parameters.
a ...... Regression coefficient (slope)
b ...... Regression constant term (intercept)
r ...... Correlation coefficient
kk
kk
k Med-Med Graph
When it is suspected that there are a number of extreme values, a Med-Med graph
can be used in place of the least squares method. This is also a type of linear regres-
sion, but it minimizes the effects of extreme values. It is especially useful in produc-
ing highly reliable linear regression from data that includes irregular fluctuations,
such as seasonal surveys.
2(Med)
123456
P.289
(Graph Type)
(Scatter)
(GPH1)
(X)
P.289
123456
To Next Page
Loading...
Need help?
General
