70
3-4 Quadratic Differential Calculations
After displaying the function analysis menu, you can input quadratic differentials
using either of the two following formats.
3(d
2
/dx
2
) f(x),a,n)
Quadratic differential calculations produce an approximate differential value using
the following second order differential formula, which is based on Newton's polyno-
mial interpretation.
–
f(x – 2h) + 16 f (x – h) – 30 f(x) + 16 f(x + h) – f(x + 2h)
f''(x)
= –––––––––––––––––––––––––––––––––––––––––––––––
12h
2
In this expression, values for “sufficiently small increments of x” are sequentially
calculated using the following formula, with the value of m being substituted as m =
1, 2, 3 and so on.
1
h = ––––
5
m
The calculation is finished when the value of f"(x) based on the value of h calcu-
lated using the last value of m, and the value of f"(x) based on the value of h
calculated using the current value of m are identical before the upper n digit is reached.
• Normally, you should not input a value for n. It is recommended that you only
input a value for n when required for calculation precision.
• Inputting a larger value for
n does not necessarily produce greater precision.
uu
uu
uTo perform a quadratic differential calculation
Example To determine the quadratic differential coefficient at the point
where x = 3 for the function y = x
3
+ 4x
2
+ x – 6
Here we will use a final boundary value of n = 6.
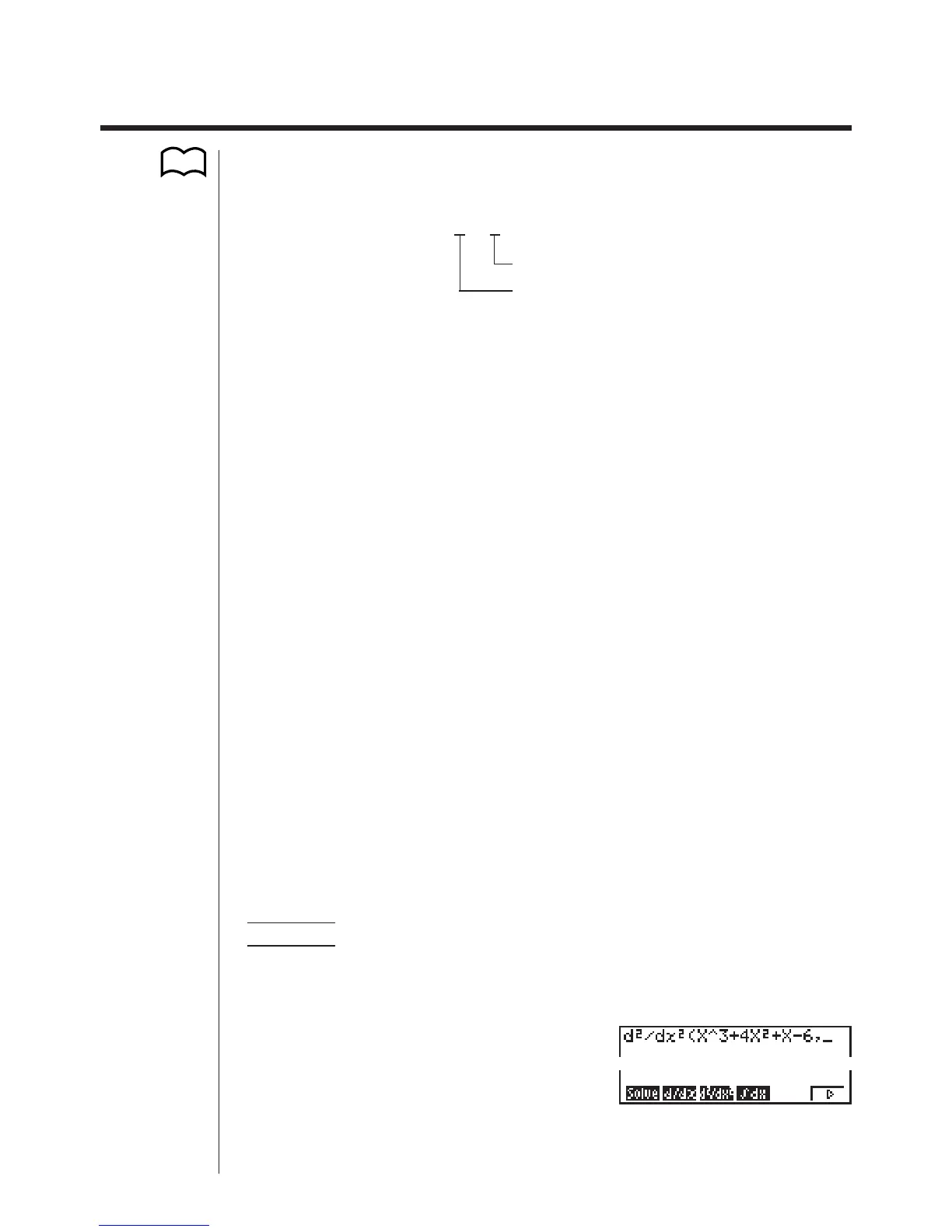
Input the function f(
x).
AK4(CALC)3(
d
2
/dx
2
)
vMd+evx+
v-g,
P.64
d
2
d
2
––– ( f (x), a, n) & ––– f (a)
dx
2
dx
2
Final boundary (
n
= 1 to 15)
Differential coefficient point
123 456
To Next Page
Loading...
Need help?
General
