HP 50G

Page 14-6
We find critical points at (X,Y) = (1,0), and (X,Y) = (-1,0). To calculate the
discriminant, we proceed to calculate the second derivatives, fXX(X,Y) = ∂
2
f/
∂X
2
, fXY(X,Y) = ∂
2
f/∂X/∂Y, and fYY(X,Y) = ∂
2
f/∂Y
2
.
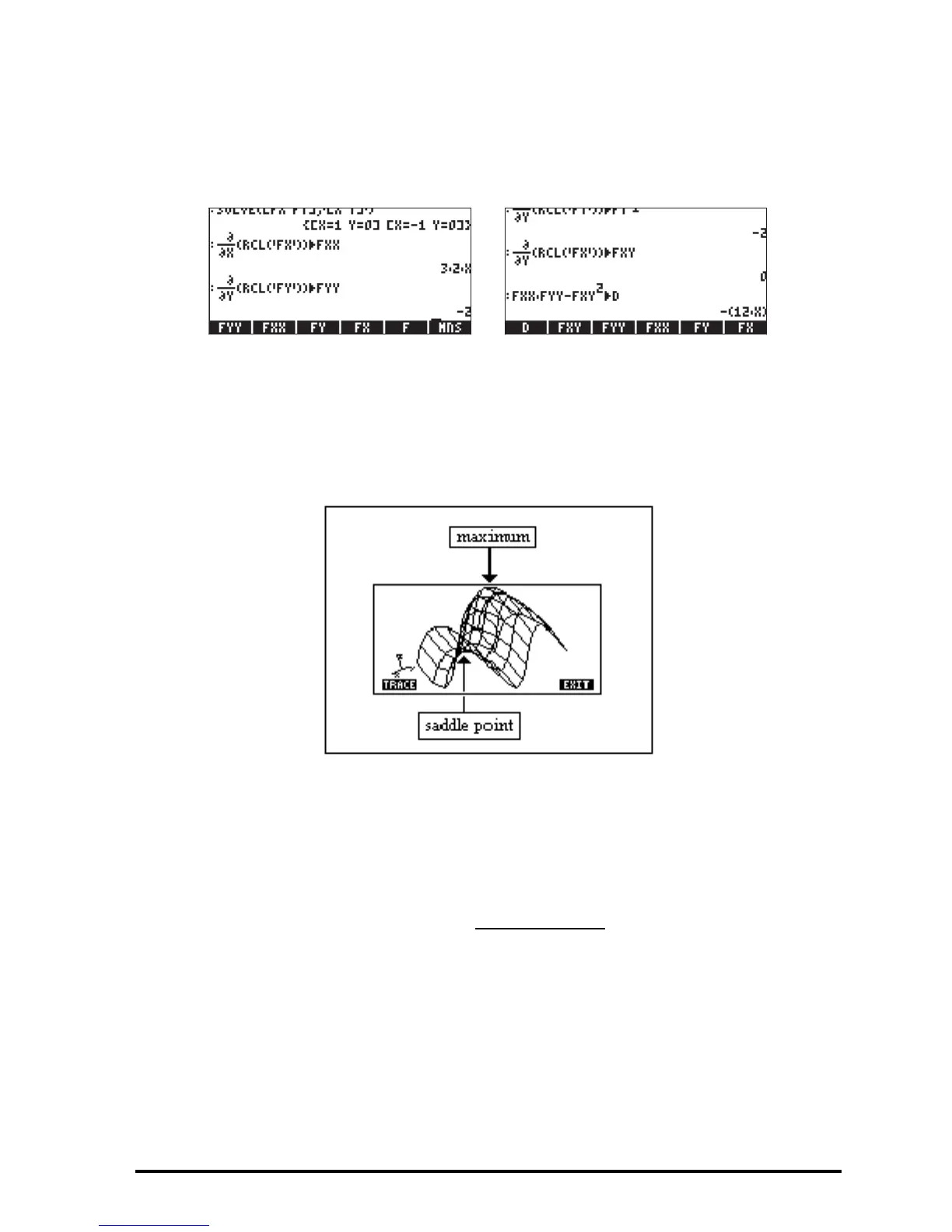
The last result indicates that the discriminant is Δ = -12X, thus, for (X,Y) = (1,0),
Δ <0 (saddle point), and for (X,Y) = (-1,0), Δ>0 and ∂
2
f/∂X
2
<0 (relative
maximum). The figure below, produced in the calculator, and edited in the
computer, illustrates the existence of these two points:
Using function HESS to analyze extrema
Function HESS can be used to analyze extrema of a function of two variables as
shown next. Function HESS, in general, takes as input a function of n
independent variables φ(x
1
, x
2
, …,x
n
), and a vector of the functions [‘x
1
’
‘x
2
’…’x
n
’]. Function HESS returns the Hessian matrix of the function φ, defined
as the matrix H = [h
ij
] = [∂
2
φ/∂x
i
∂x
j
], the gradient of the function with respect to
the n-variables, grad f = [ ∂φ/∂x
1
, ∂φ/∂x
2
, … ∂φ/∂x
n
], and the list of
variables [‘x
1
’ ‘x
2
’…’x
n
’].