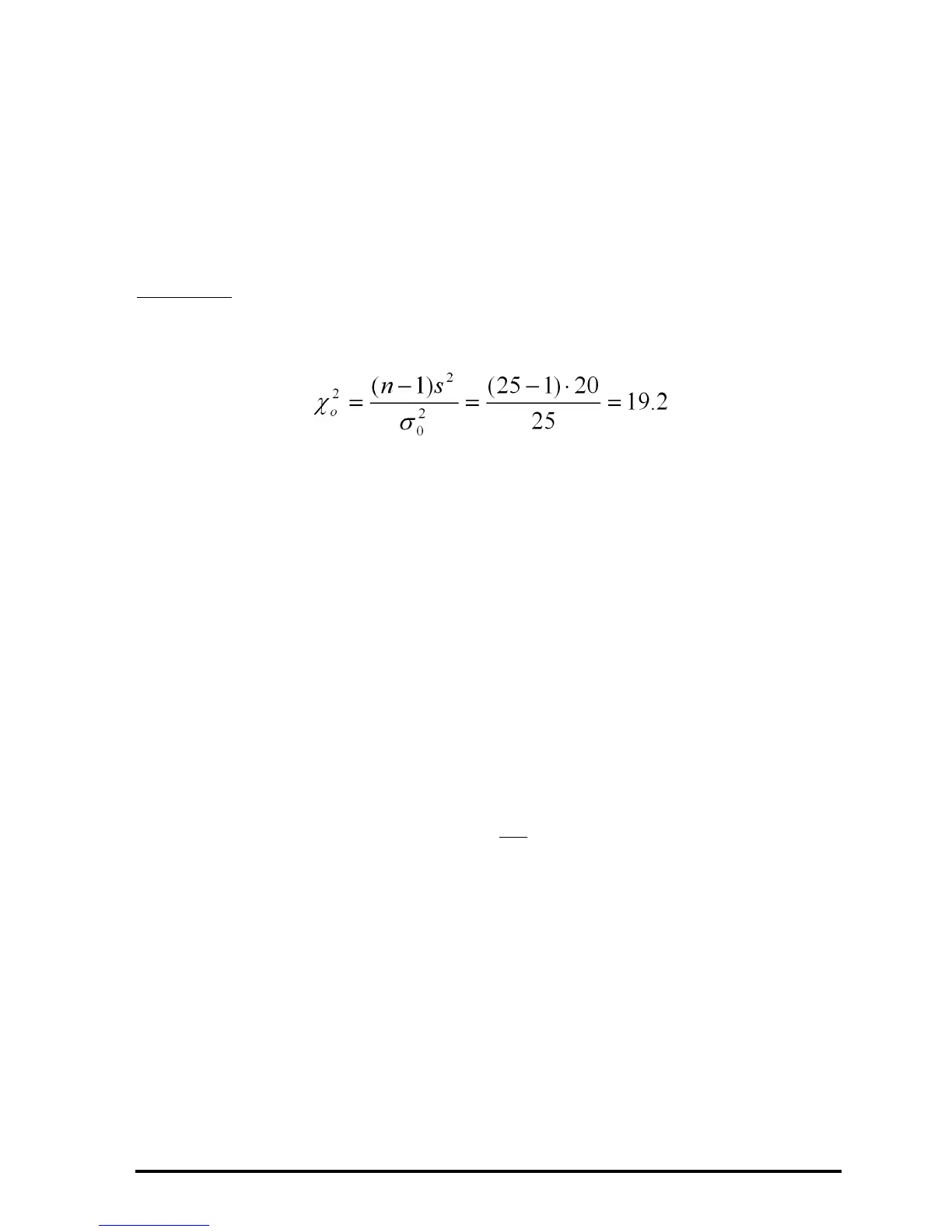HP 50G

Page 18-48
The test criteria are the same as in hypothesis testing of means, namely,
Θ Reject H
o
if P-value < α
Θ Do not reject H
o
if P-value > α.
Please notice that this procedure is valid only if the population from which the
sample was taken is a Normal population.
Example 1
-- Consider the case in which σ
o
2
= 25, α=0.05, n = 25, and s
2
=
20, and the sample was drawn from a normal population. To test the
hypothesis, H
o
: σ
2
= σ
o
2
, against H
1
: σ
2
< σ
o
2
, we first calculate
With ν = n - 1 = 25 - 1 = 24 degrees of freedom, we calculate the P-value as,
P-value = P(χ
2
<19.2) = 1-UTPC(24,19.2) = 0.2587…
Since, 0.2587… > 0.05, i.e., P-value > α, we cannot reject the null hypothesis,
H
o
: σ
2
=25(= σ
o
2
).
Inferences concerning two variances
The null hypothesis to be tested is , H
o
: σ
1
2
= σ
2
2
, at a level of confidence (1-
α)100%, or significance level α, using two samples of sizes, n
1
and n
2
, and
variances s
1
2
and s
2
2
. The test statistic to be used is an F test statistic defined
as
where s
N
2
and s
D
2
represent the numerator and denominator of the F statistic,
respectively. Selection of the numerator and denominator depends on the
alternative hypothesis being tested, as shown below. The corresponding F
distribution has degrees of freedom, ν
N
= n
N
-1, and ν
D
= n
D
-1, where n
N
and
n
D
, are the sample sizes corresponding to the variances s
N
2
and s
D
2
,
respectively.
2
2
D
N
o
s
s
F =