RM0440 Rev 4 475/2126
RM0440 CORDIC co-processor (CORDIC)
485
required, it has to be calculated in software and programmed into the SCALE field of the
CORDIC_CSR register. The input arguments must be scaled accordingly before
programming the scaled values in the CORDIC_WDATA register. The scaling must also be
undone on the results read from the CORDIC_RDATA register.
Note: The scaling factor entails a loss of precision due to truncation of the scaled value.
17.3.5 Precision
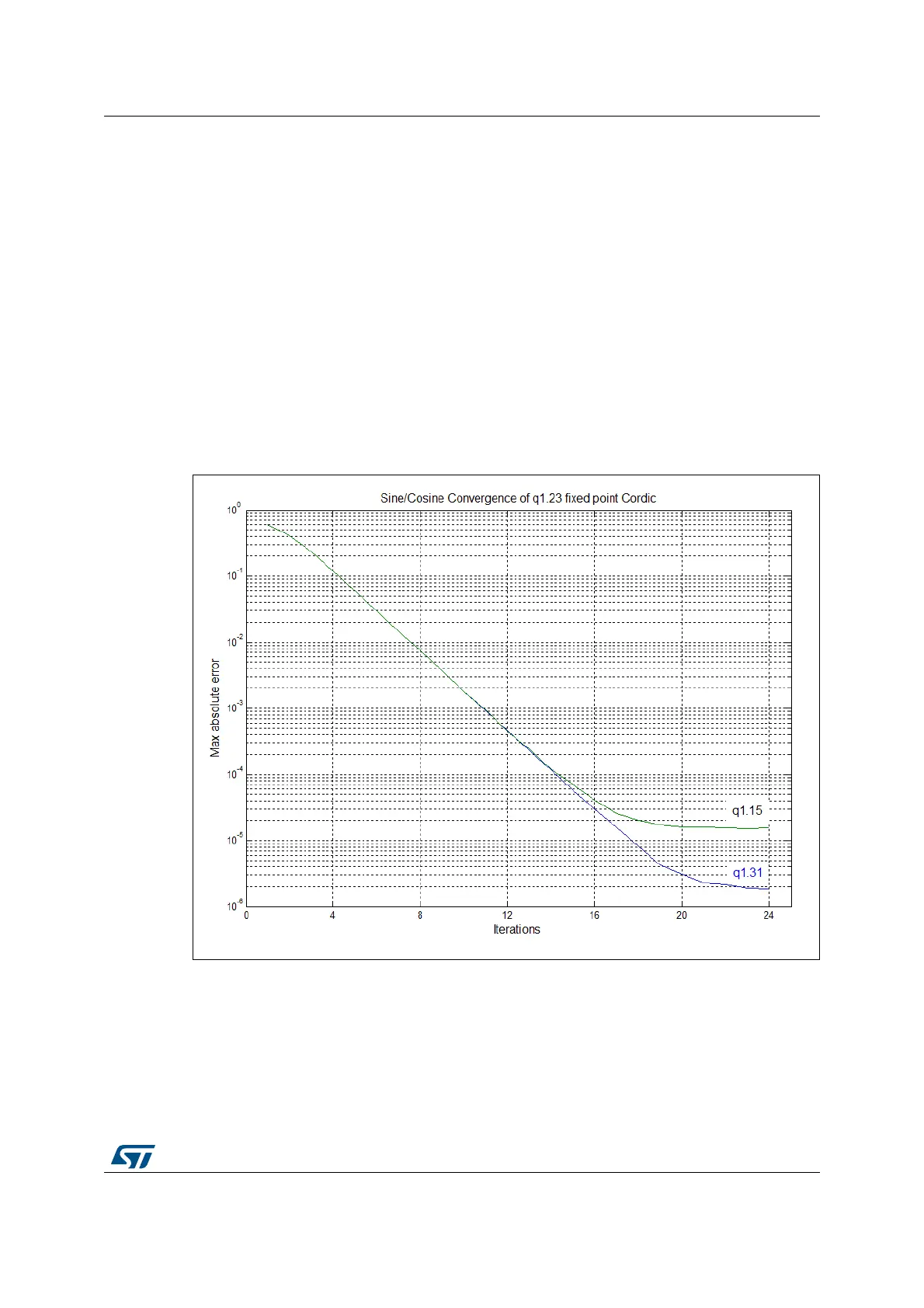
The precision of the result is dependent on the number of CORDIC iterations. The algorithm
converges at a constant rate of one binary digit per iteration for trigonometric functions
(sine, cosine, phase, modulus), see Figure 38.
For hyperbolic functions (hyperbolic sine, hyperbolic cosine, natural logarithm), the
convergence rate is less constant due to the peculiarities of the CORDIC algorithm (see
Figure 39). The square root function converges at roughly twice the speed of the hyperbolic
functions (see Figure 40).
Figure 38. CORDIC convergence for trigonometric functions
To Next Page
Loading...
Need help?
General
