IQmath
8 - 16 C2000 Microcontroller Workshop - Numerical Concepts
IQmath
Implementing complex digital control algorithms on a Digital Signal Processor (DSP), or any
other DSP capable processor, typically come across the following issues:
• Algorithms are typically developed using floating-point math
• Floating-point devices are more expensive than fixed-point devices
• Converting floating-point algorithms to a fixed-point device is very time consuming
• Conversion process is one way and therefore backward simulation is not always possible
The design may initially start with a simulation (i.e. MatLab) of a control algorithm, which
typically would be written in floating-point math (C or C++). This algorithm can be easily ported
to a floating-point device, however because of cost reasons most likely a 16-bit or 32-bit fixed-
point device would be used in many target systems.
The effort and skill involved in converting a floating-point algorithm to function using a 16-bit or
32-bit fixed-point device is quite significant. A great deal of time (many days or weeks) would
be needed for reformatting, scaling and coding the problem. Additionally, the final
implementation typically has little resemblance to the original algorithm. Debugging is not an
easy task and the code is not easy to maintain or document.
IQ Fractional Representation
A new approach to fixed-point algorithm development, termed “IQmath”, can greatly simplify the
design development task. This approach can also be termed “virtual floating-point” since it looks
like floating-point, but it is implemented using fixed-point techniques.
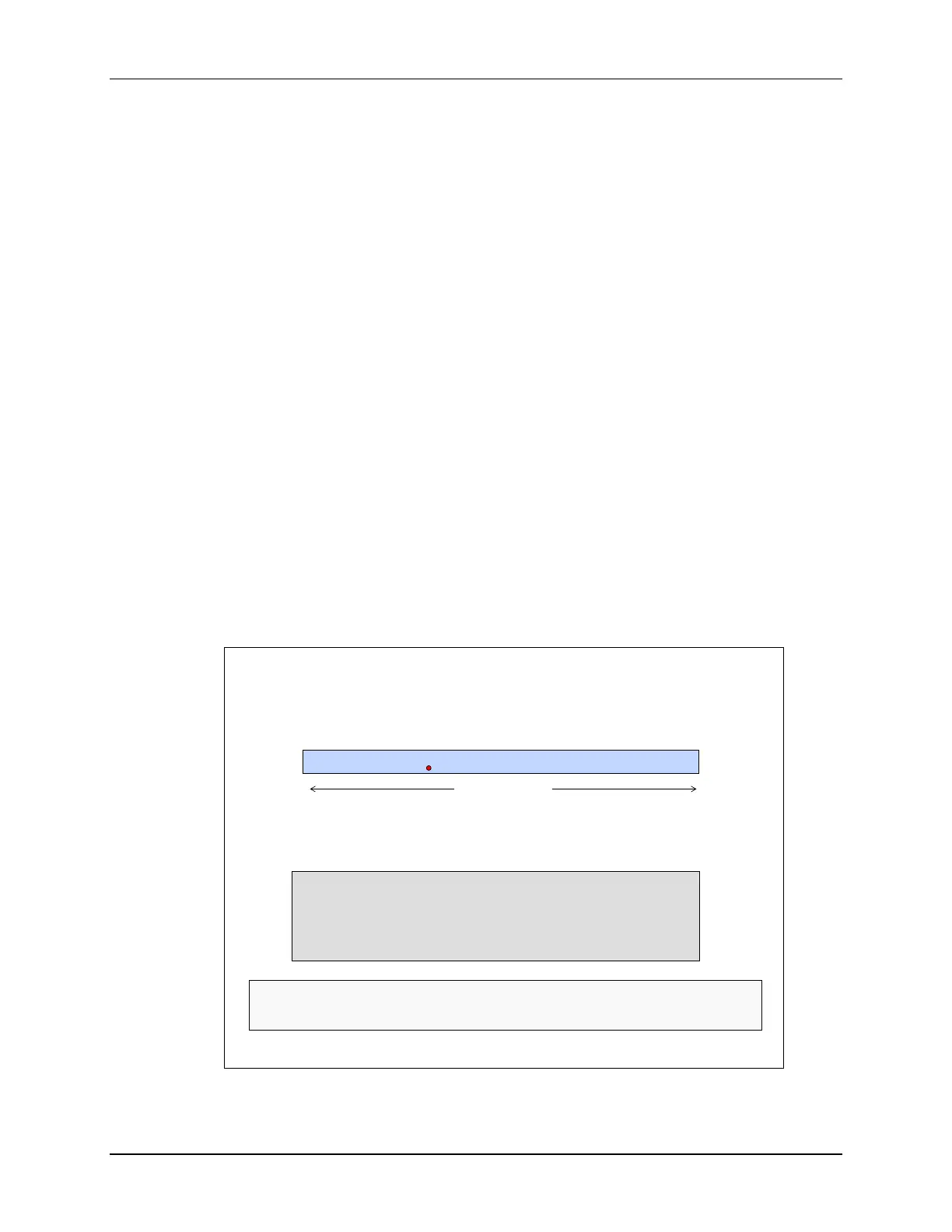
IQ Fractional Representation
S IIIIIIII
fffffffffffffffffffffff
031
32 bit mantissa
Advantage ⇒ Precision same for all numbers in an IQ format
Disadvantage ⇒ Limited dynamic range compared to floating-point
-2
I
+ 2
I-1
+ … + 2
1
+ 2
0
.2
-1
+ 2
-2
+ … + 2
-Q
I8Q24 Example: 0x41200000
= 0100 0001 . 0010 0000 0000 0000 0000 0000 b
= 2
6
+ 2
0
+ 2
-3
= 65.125

 Loading...
Loading...











