3.28 Function Graphing
82533F~1.DOC TI-83 international English Bob Fedorisko Revised: 10/26/05 1:20 PM Printed: 10/27/05 1:55
PM Page 28 of 28
82533F~1.DOC TI-83 international English Bob Fedorisko Revised: 10/26/05 1:20 PM Printed: 10/27/05 1:55
PM Page 28 of 28
dy/dx (numerical derivative) finds the numerical derivative
(slope) of a function at a point, with H=1âL3.
To find a function’s slope at a point, follow these steps.
1. Select
6:dy/dx from the CALCULATE menu. The current
graph is displayed.
2. Press } or † to select the function for which you want to
find the numerical derivative.
3. Press | or ~ (or enter a value) to select the
X value at
which to calculate the derivative, and then press Í.
The cursor is on the solution and the numerical derivative is
displayed.
To move to the same x-value for other selected functions, press
} or †. To restore the free-moving cursor, press | or ~.
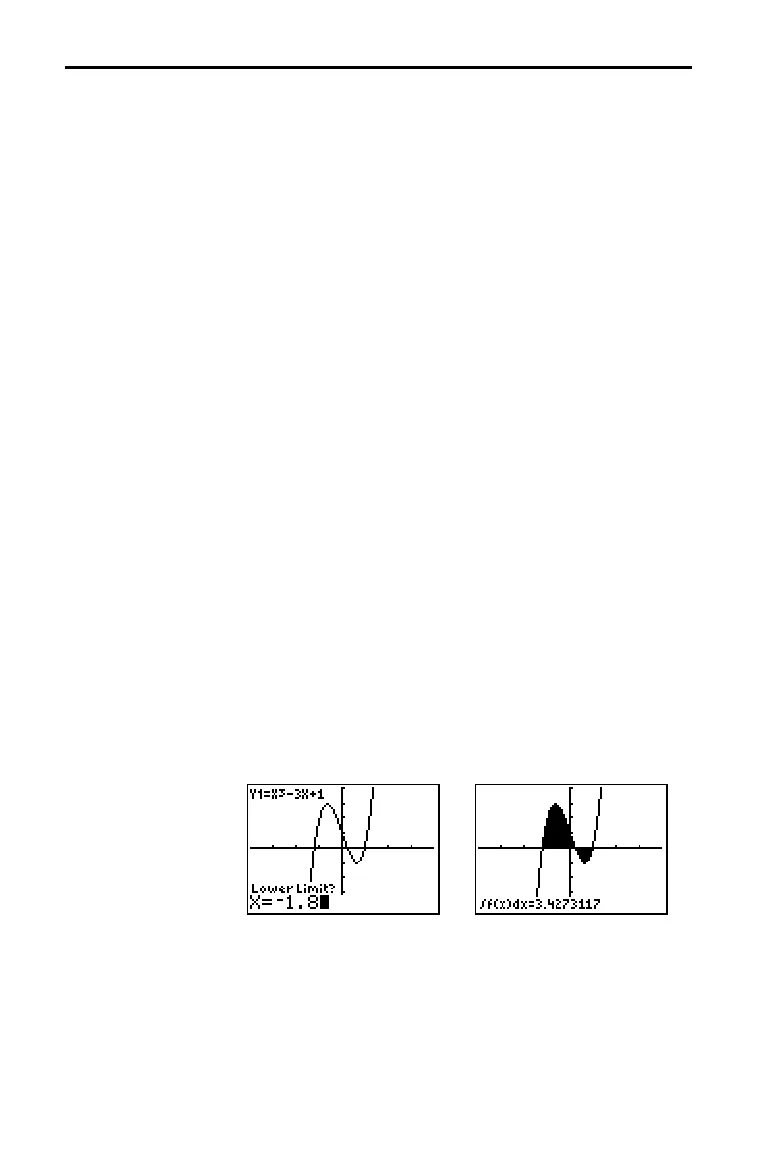
‰f(x)dx (numerical integral) finds the numerical integral of a
function in a specified interval. It uses the
fnInt( function, with a
tolerance of H=1âL3.
To find the numerical derivative of a function, follow these
steps.
1. Select
7:‰f(x)dx from the CALCULATE menu. The current
graph is displayed with
Lower Limit? in the bottom-left
corner.
2. Press } or † to move the cursor to the function for which
you want to calculate the integral.
3. Set lower and upper limits as you would set left and right
bounds for
zero (step 3; page 3.26). The integral value is
displayed, and the integrated area is shaded.
Note: The shaded area is a drawing. Use ClrDraw (Chapter 8) or
any action that invokes Smart Graph to clear the shaded area.
Using the CALC (Calculate) Operations (continued)
dy/dx
‰f(x)dx
To Next Page
Loading...
Need help?
General
