17–14 Applications
82501F~1.DOC TI-83 international English Bob Fedorisko Revised: 10/26/05 1:49 PM Printed: 10/27/05 3:04
PM Page 14 of 20
Using the functions fnInt( and nDeriv( from the MATH menu to
graph functions defined by integrals and derivatives
demonstrates graphically that:
F(x) =
‰
1
x
1Ã t dt = ln(x), x > 0 and that
D
x
[‰
1
x
1Ã t dt] = 1Ã x
1. Press z. Select the default settings.
2. Press p. Set the viewing window.
Xmin=.01 Ymin=M1.5 Xres=3
Xmax=10 Ymax=2.5
Xscl=1 Yscl=1
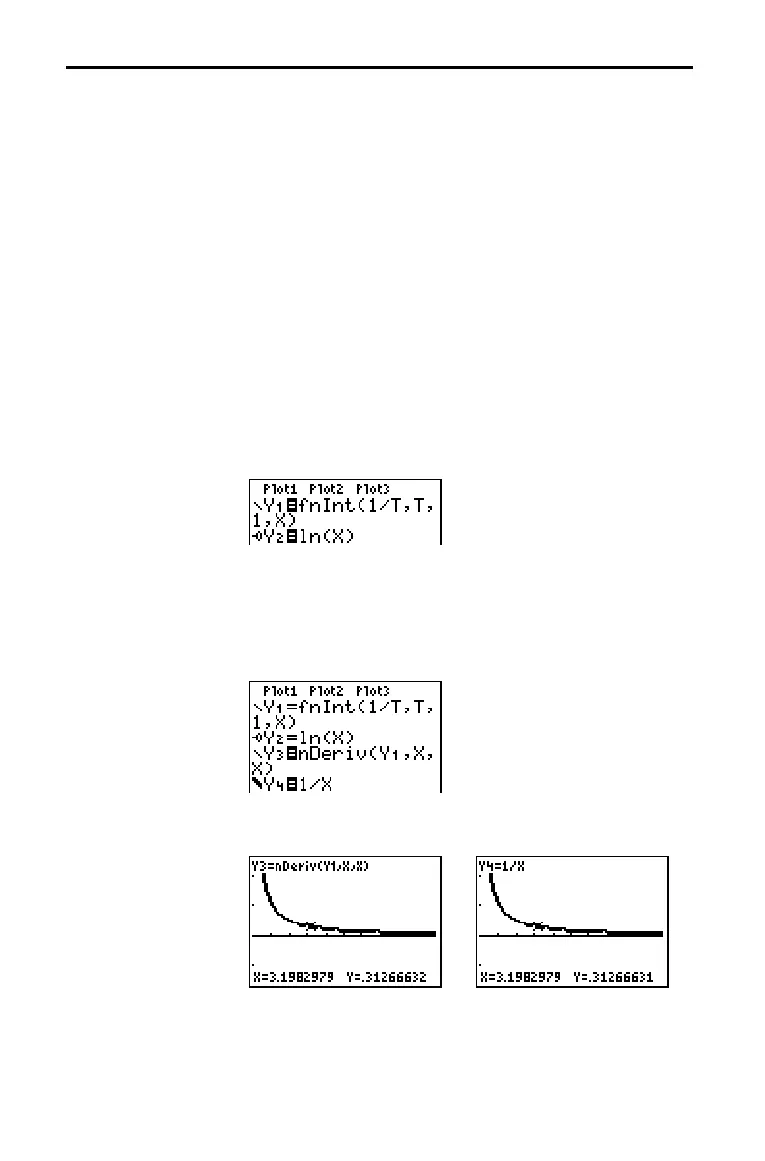
3. Press o. Turn off all functions and stat plots. Enter the
numerical integral of 1Ã T from 1 to X and the function
ln(X). Set the graph style for
Y1 to ç (line) and Y2 to
ë (path).
4. Press r. Press |, }, ~, and †to compare the values
of
Y1 and Y2.
5. Press o. Turn off Y1 and Y2, and then enter the numerical
derivative of the integral of 1Ã X and the function 1Ã X. Set
the graph style for
Y3 to ç
çç
ç (line) and Y4 to è
èè
è (thick).
6. Press r. Again, use the cursor keys to compare the
values of the two graphed functions,
Y3 and Y4.
Demonstrating the Fundamental Theorem of Calculus
Problem 1
Procedure 1
To Next Page
Loading...
Need help?
General
