PID TUTORIAL
FMS-1650
TRIATEK reserves the right to change product specifications without notice.
- 64 -
PID is an acronym that stands for Proportional-Integral-Derivative, and
is a generic closed-loop control mechanism that is commonly used in
many industrial control systems. It is by far the most commonly used
feedback controller in use today. A controller which implements PID
mode continuously calculates the difference (or error signal) between
a measured process variable (PV) and a desired setpoint (SP). The
PID controller attempts to minimize this error by adjusting the process
control inputs, also referred to as the manipulated variable (MV). A
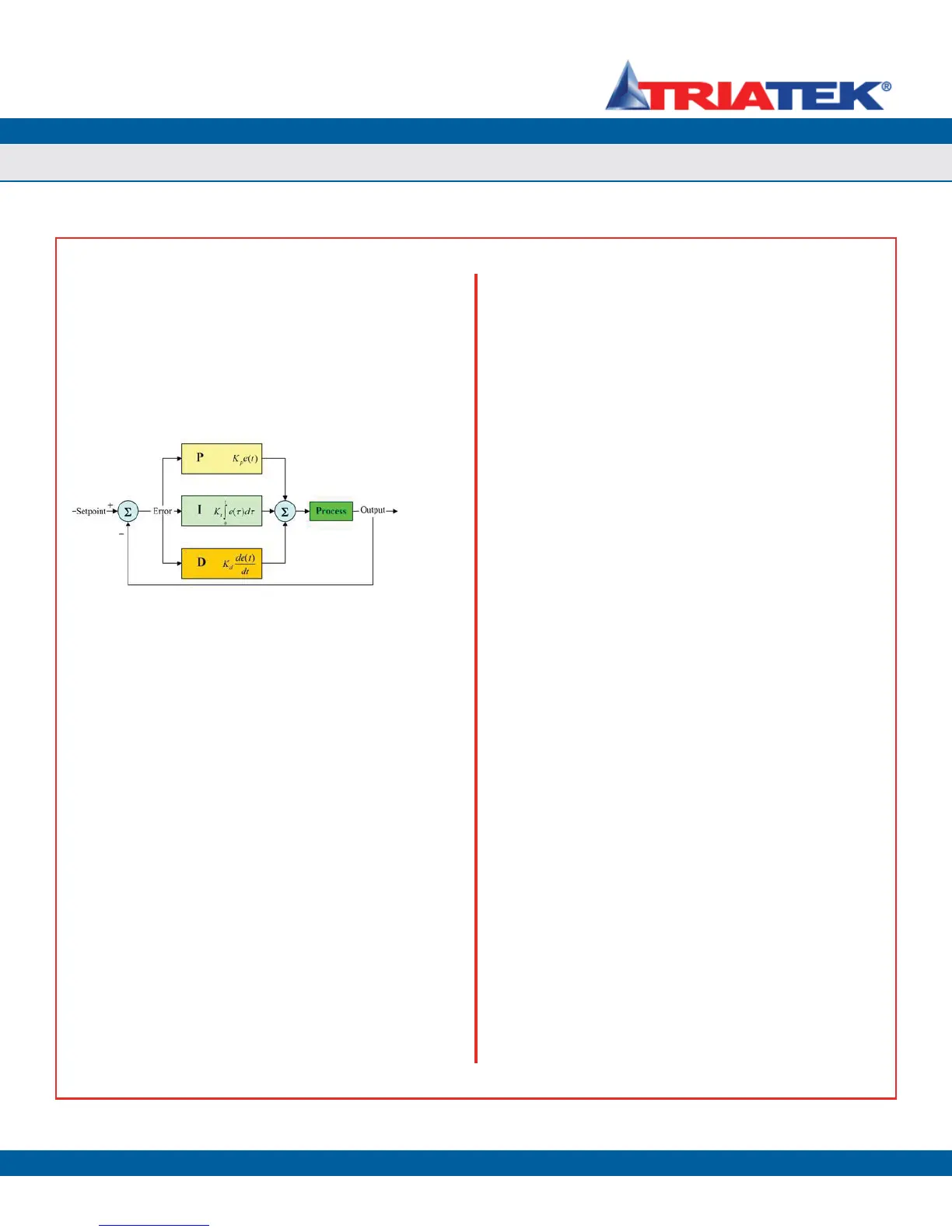
block diagram of a PID controller is shown in Figure 106.
The PID controller algorithm consists of three parameters: proportional,
integral, and derivative. In terms of time, the proportional term
depends on the present error, the integral term depends on the
accumulation of past errors, and the derivative term is a prediction
of future errors. The weighted sum of these three terms is used to
adjust the process via a control variable such as the position of a
control valve of the power applied to a heating element. In the case
of applications for the FMS-1650 as a room pressure controller, the
process variable is the differential pressure and the control variable is
typically the position of an exhaust damper.
By tuning the PID parameters or constants in the algorithm, the
controller can provide control action designed for specific process
requirements. The response of the controller can be described in
terms of the responsiveness of the controller to an error, the degree
to which the controller overshoots the setpoint, and the degree of
system oscillation. Some applications may require using only one or
two terms to provide the appropriate system control. This is achieved
by setting the constant(s) of the undesired control output(s) to zero.
The variations include PI, PD, P, or I controllers in the absence of the
respective control actions. PI controllers are relatively common, since
the derivative term is sensitive to measurement noise, whereas the
absence of an integral value may prevent the system from reaching its
target value due to the control action.
A typical example of a closed-loop control scheme is when the hot
and cold valves of a faucet are adjusted to maintain the water from the
faucet at a desired temperature. This involves the mixing of the two
process streams, the hot and cold water. Touching the water allows
the temperature to be sensed or “measured.” Based on this feedback
of sensing the water temperature, a control action may be performed
to adjust the hot and cold water valves until the process temperature
stabilizes at the desired value.
Sensing the water temperature is analogous to taking a measurement
of the process variable (PV), while the desired temperature is referred
to as the setpoint (SP). The input to the process (water valve position)
is referred to as the manipulated variable (MV). The difference
between the “measured” temperature and the setpoint is the error (e)
and quantifies whether the water is too hot or too cold, and by how
much. After measuring the temperature (PV), and then calculating
the error, the controller decides when to change the tap position (MV)
and by how much. When the controller first turns the valve on, it may
turn the hot valve only slightly if warm water is desired, or it may open
the valve all the way if very hot water is desired. This is an example
of a simple proportional control. In the event that hot water does
not arrive quickly, the controller may try to speed-up the process by
opening up the hot water valve more as time goes by. This is an
example of an integral control.
PID Controller Theory
The PID closed-loop control scheme is named after its three correcting
terms, whose sum constitutes the manipulated variable (MV):
MV(t) = P
out
+ I
out
+ D
out
where P
out
, I
out
,
and D
out
are the contributions to the output from
the PID controller from each of the three terms, as defined in the
subsequent sections below.
Proportional Term
The proportional term (sometimes referred to as gain) makes a change
to the output that is proportional to the current error value. The
proportional response can be adjusted by multiplying the error by a
constant K
p
called the proportional gain. The proportional term of the
output is given by:
K
p
: proportional constant (tuning parameter)
SP: setpoint or desired value
Figure 106. Block
diagram of a PID
controller.
TRIATEK reserves the right to change product specifications without notice.
PID Tutorial
 Loading...
Loading...