215
To
represent the floating point values, the rightmost seven
digits are used for the
mantissa
and the leftmost digit is used
for the exponent, as shown below
. The
mantissa is expressed as a value less than one, i.e., to seven decimal places.
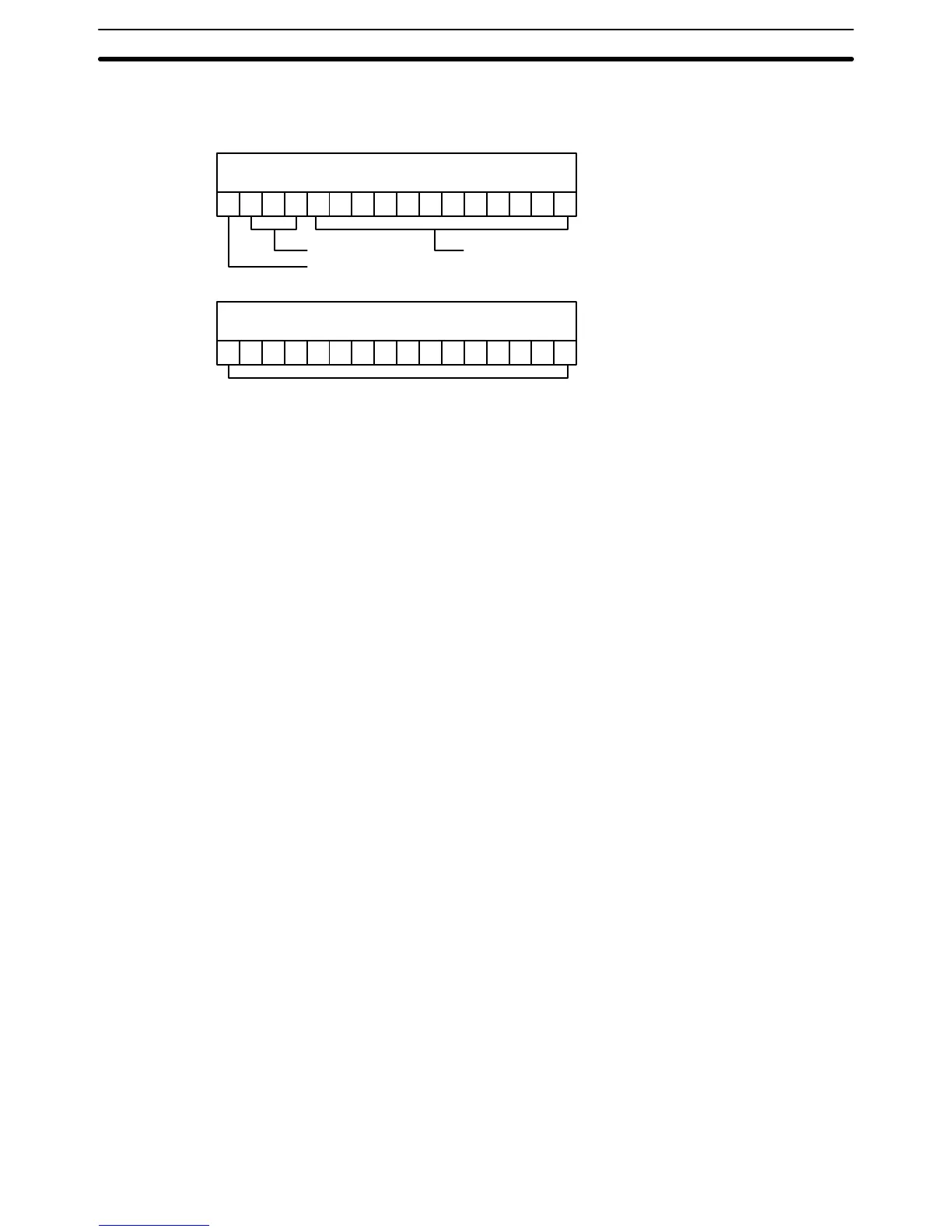
15 14 13 12 11 10 09 08 07 06 05 04 03 02 01 00
First
word
exponent
(0 to 7)
sign of exponent
0: +
1: –
1010000100010001
mantissa (leftmost 3 digits)
15 14 13 12 11 10 09 08 07 06 05 04 03 02 01 00
Second word
mantissa (leftmost 4 digits)
0001000100010001
= 0.1111111 x 10
–2
Flags ER: Dr and Dr+1 contain 0.
Dd, Dd+1, Dr, or Dr+1 is not BCD.
The result is not between 0.1 x 10
–7
and 0.999999 x 10
7
.
Indirectly
addressed DM word
is non-existent. (Content of *DM word is
not BCD, or the DM area boundary has been exceeded.)
EQ: ON when the result is 0.
Example The
following example shows how to divide
two whole four-digit numbers (i.e.,
numbers without fractions) so that a floating-point value can be obtained.
First the original numbers must be placed in floating-point form. Because the
numbers
are
originally without decimal points, the exponent will be 4 (e.g., 3452
would
equal 0.3452 x 10
4
). All of the moves are to place the proper data into con
-
secutive words for the final division, including the exponent and zeros. Data
movements for Dd and Dd+1 are shown at the right below. Movements for Dr
and Dr+1 are basically the same.The original values to be divided are in DM
0000 and DM 0001. The final division is also shown.
BCD Calculations Section 5-19
To Next Page
Loading...
Need help?
General
