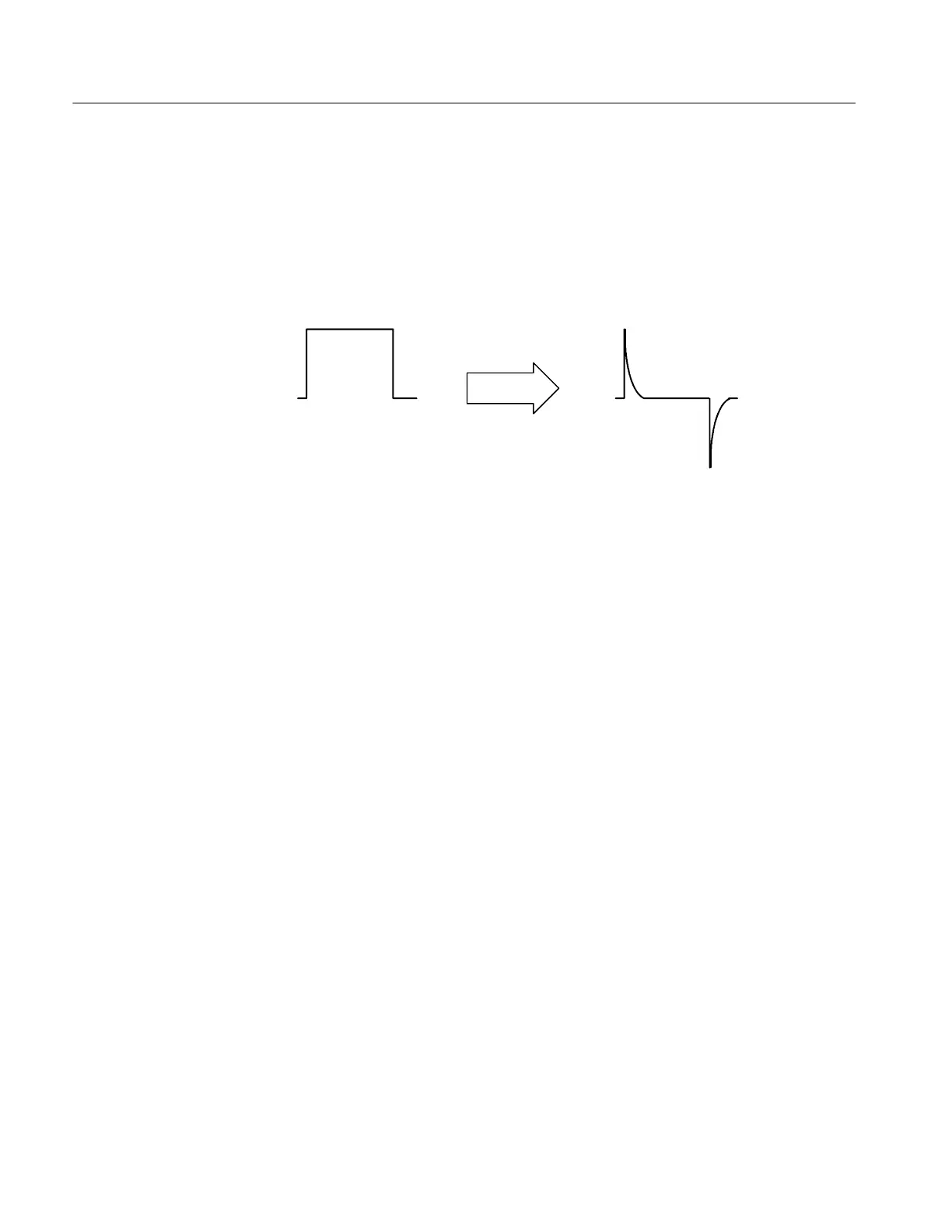Creating and Using Math Waveforms
3- 168
CSA7000B Series & TDS7000B Series Instruments User Manual
Defining Math Waveforms
This instrument supports mathematical combination and functional transforma-
tions of waveforms it acquires. Figure 3--44 shows this concept:
Channel waveform
(Ch2)
Math waveform
(Math1)
Diff(Ch2)
Math expression
(Function(source))
Figure 3- 44: Functional transformation of an acquired waveform
You create math waveforms to support the analysis of your channel and reference
waveforms. By combining and transforming source waveforms and other data
into math waveforms, you can derive the data view that your application
requires. You can create math waveforms that result from:
H Mathematical operations on one or several waveforms: add, subtract,
multiply, and divide
H Logical operations: greater than, less than, less than or equal, greater than or
equal, not equal or equal
H Variables that you set
H Regular scalars such as 3.14
H Function transforms of waveforms, s uch as integrating, differentiating, and
so on
H Spectral analysis of waveforms, such as an impulse
H Measurement scalars can be used in expression; for example, you can use the
measurement feature this instrument provides to measure the average of a
waveform and subtract it from the original waveform to define a new math
waveform
You can create up to four math waveforms; see Using Math on page 3--169 for
more examples.
Math waveforms can be used in other math. Math waveforms autoscale when the
math waveform is first defined and turned on. Advanced functions, such as
To Next Page
Loading...
Need help?
General
