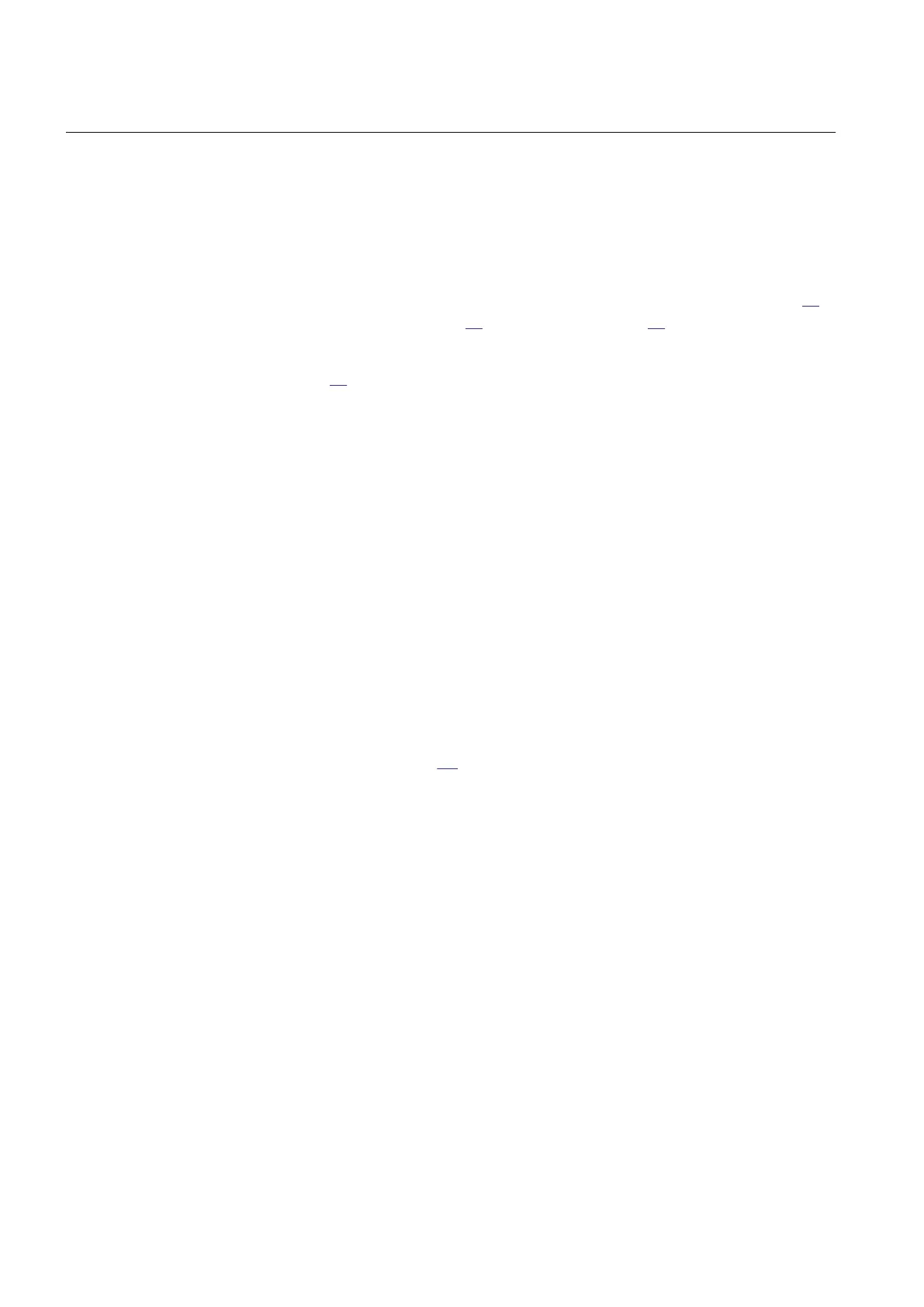p
2
p Re K
1
( ) Re K
2
( ) R
F
Re K
3
( ) 0=×–+×–
EQUATION107 V1 EN-US (Equation 91)
p Im K
1
( ) Im K
2
( ) R
F
Im K
3
( ) 0=× ×–×+× ×–
EQUATION108 V1 EN-US (Equation 92)
If the imaginary part of K
3
is not zero, R
F
can be solved according to equation 92,
and then inserted to equation
91. According to equation 91, the relative distance to
the fault is solved as the root of a quadratic equation.
Equation 91 gives two different values for the relative distance to the fault as a
solution. A simplified load compensated algorithm, which gives an unequivocal
figure for the relative distance to the fault, is used to establish the value that should
be selected.
If the load compensated algorithms according to the above do not give a reliable
solution, a less accurate, non-compensated impedance model is used to calculate
the relative distance to the fault.
14.9.7.3 The non-compensated impedance model
M14983-121 v3
In the non-compensated impedance model, I
A
line current is used instead of I
FA
fault current:
EQUATION109 V1 EN-US (Equation 93)
Where:
I
A
is according to table 442.
The accuracy of the distance-to-fault calculation, using the non-compensated
impedance model, is influenced by the pre-fault load current. So, this method is
only used if the load compensated models do not function.
14.9.7.4 IEC 60870-5-103
M14983-135 v2
The communication protocol IEC 60870-5-103 may be used to poll fault location
information from the IED to a master (that is station HSI). There are two outputs
that must be connected to appropriate inputs on the function block I103StatFltDis,
FLTDISTX gives distance to fault (reactance, according the standard) and
CALCMADE gives a pulse (100 ms) when a result is obtainable on FLTDISTX
output.
Section 14 1MRK 506 382-UEN A
Monitoring
630 Line distance protection REL650 2.2 IEC
Technical manual
 Loading...
Loading...