3-96 Full Command and Function Reference
for the complex-valued natural log function occurs where the corresponding real-valued function
is undefined. The principal branch also preserves most of the important symmetries.
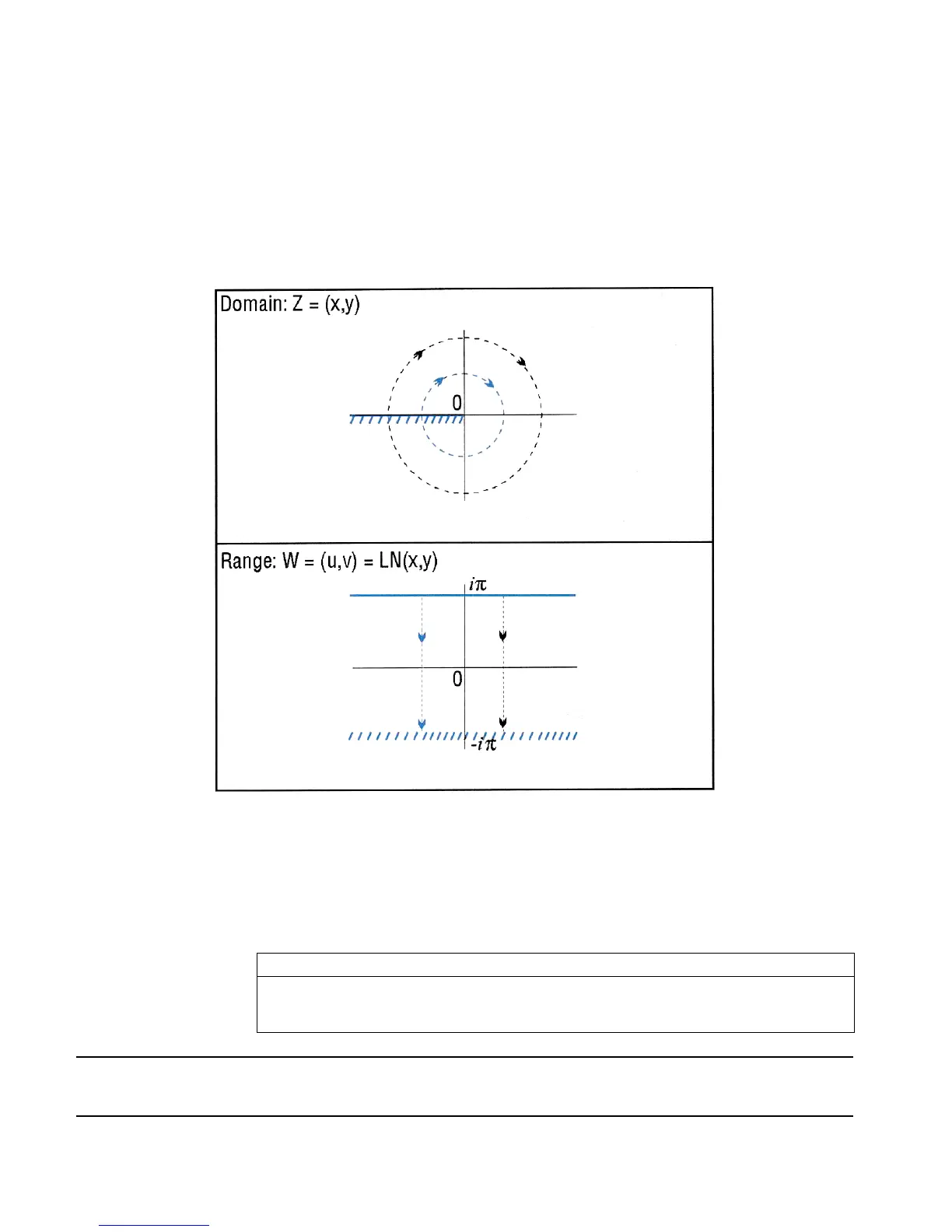
The graphs below show the domain and range of LN. The graph of the domain shows where the
branch cut occurs: the heavy solid line marks one side of the cut, while the feathered lines mark
the other side of the cut. The graph of the range shows where each side of the cut is mapped
under the function.
These graphs show the inverse relation LN(Z)+2*π*i*n1 for the case n1=0. For other values of
n1, the horizontal band in the lower graph is translated up (for n1 positive) or down (for n1
negative). Taken together, the bands cover the whole complex plane, which is the domain of
EXP.
You can view these graphs with domain and range reversed to see how the domain of EXP is
restricted to make an inverse function possible. Consider the vertical band in the lower graph as
the restricted domain Z = (x,y). EXP sends this domain onto the whole complex plane in the
range W = (u,v) = EXP(x,y) in the upper graph.
Access: …¹ (¹is the right-shift of the Qkey).
Flags: Principal Solution (-1), Numerical Results (-3), Inifinite Result Exception (-22)
Input/Output:
Level 1/Argument 1 Level 1/Item 1
z
→
ln z
'symb'
→
'LN(symb)'
See also: ALOG, EXP, ISOL, LNP1, LOG
LNAME
CAS: Return a list of variable names contained in a symbolic expression.
 Loading...
Loading...