HP 48GII

Full Command and Function Reference 3-193
Γ
z
2
---
⎝⎠
⎛⎞
z
2
---1–
⎝⎠
⎛⎞
!=
Description: Upper Snedecor's F Distribution Command: Returns the probability utpf(n
1
, n
2
, x) that a
Snedecor
's F random variable is greater than x, where n
1
and n
2
are the numerator and
denominator degrees of freedom of the F distribution.
The defining equations for utpf(n
1
, n
2
, x) are these:
• For x ≥ 0:
n
1
n
2
-----
⎝⎠
⎛⎞
n
1
2
-----
Γ
n
1
n
2
+
2
-----------------
⎝⎠
⎛⎞
Γ
n
1
2
-----
⎝⎠
⎛⎞
Γ
n
2
2
-----
⎝⎠
⎛⎞
------------------------------
t
n
1
2–
2
--------------
x
∞
∫
1
n
1
n
2
-----
⎝⎠
⎛⎞
t+
n
1
n
2
+()
2
-----------------------
–
dt
• For x < 0:
u
t
p
f
n
1
n
2
x
,,()1=
For any value z, , where ! is the hp49g+/hp48gII factorial command.
The values n
1
and n
2
are rounded to the nearest integers and, when rounded, must be positive.
Access: !´
L PROBABILITY L UTPF ( ´ is the left-shift of the Pkey).
Input/Output:
Level 3/Argument 1 Level 2/Argument 2 Level 1/Argument 3 Level 1/Item 1
n
1
n
2
x
→
utpf(n
1
,n
2
,x)
See also: UTPC, UTPN, UTPT
UTPN
Type: Command
Description: Upper Normal Distribution Command: Returns the probability utpn(m, v, x) that a normal
random variable is greater than x, where m and v are the mean and variance, respectively, of the
normal distribution.
For all x and m, and for v > 0, the defining equation is this:
utpn m v x,,()
1
2πv
-------------
e
tm–()
2
2v
- ------ ---- -------–
td
x
∞
∫
=
For v = 0, UTPN returns 0 for x ≥ m, and 1 for x < m.
Access: !´
L PROBABILITY L UTPN ( ´ is the left-shift of the Pkey).
Input/Output:
Level 3/Argument 1 Level 2/Argument 2 Level 1/Argument 3 Level 1/Item 1
m v x
→
utpn(m,v,x)
See also: UTPC, UTPF, UTPT
UTPT
Type: Command
Description: Upper Student
's t Distribution Command: Returns the probability utpt(n, x) that a Student's t
random variable is greater than x, where n is the number of degrees of freedom of the
distribution.
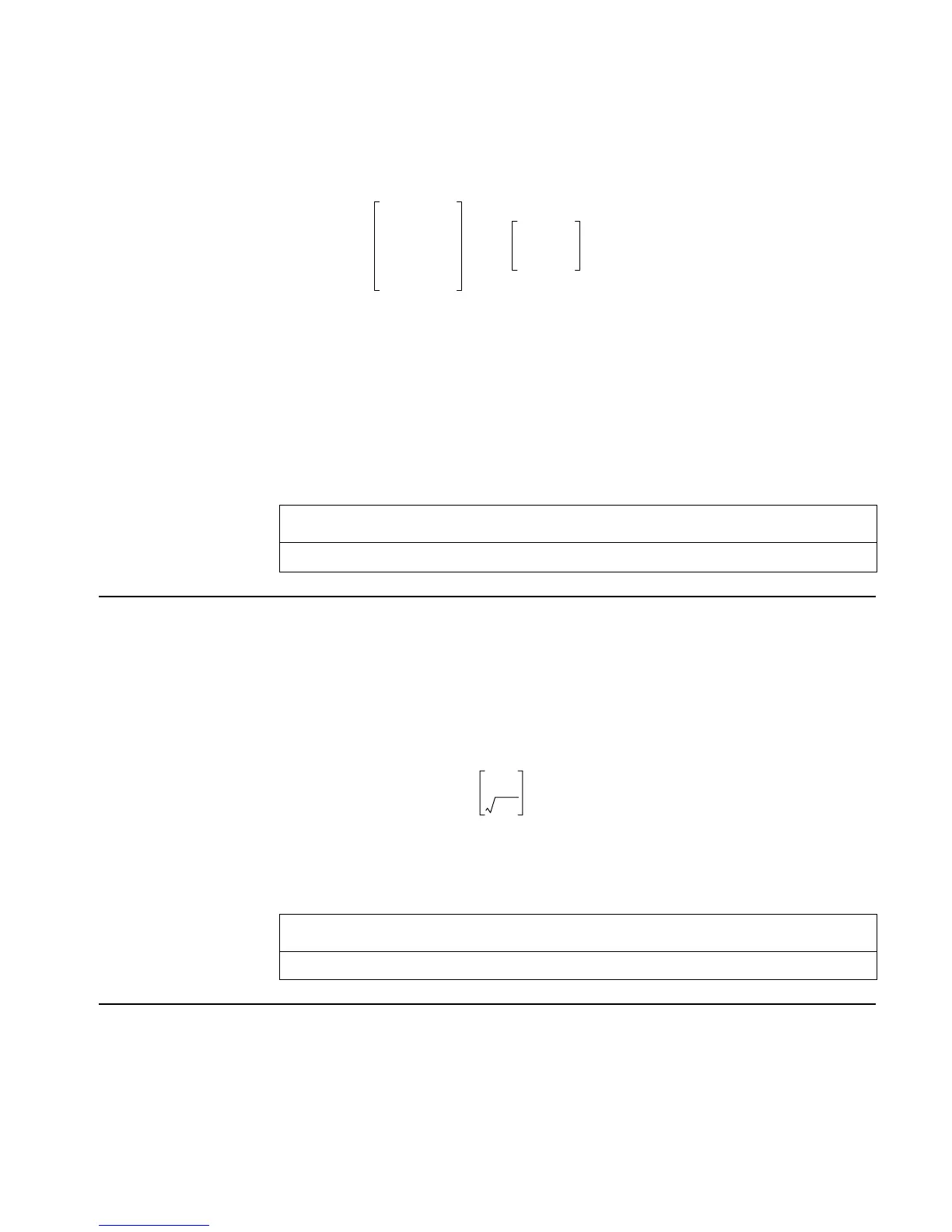
The following is the defining equation for all x: