81
Polyend Tracker Manual
80
Polyend Tracker Manual
NOTESNOTES
Sequencing Steps
5
Sequencing Steps
5
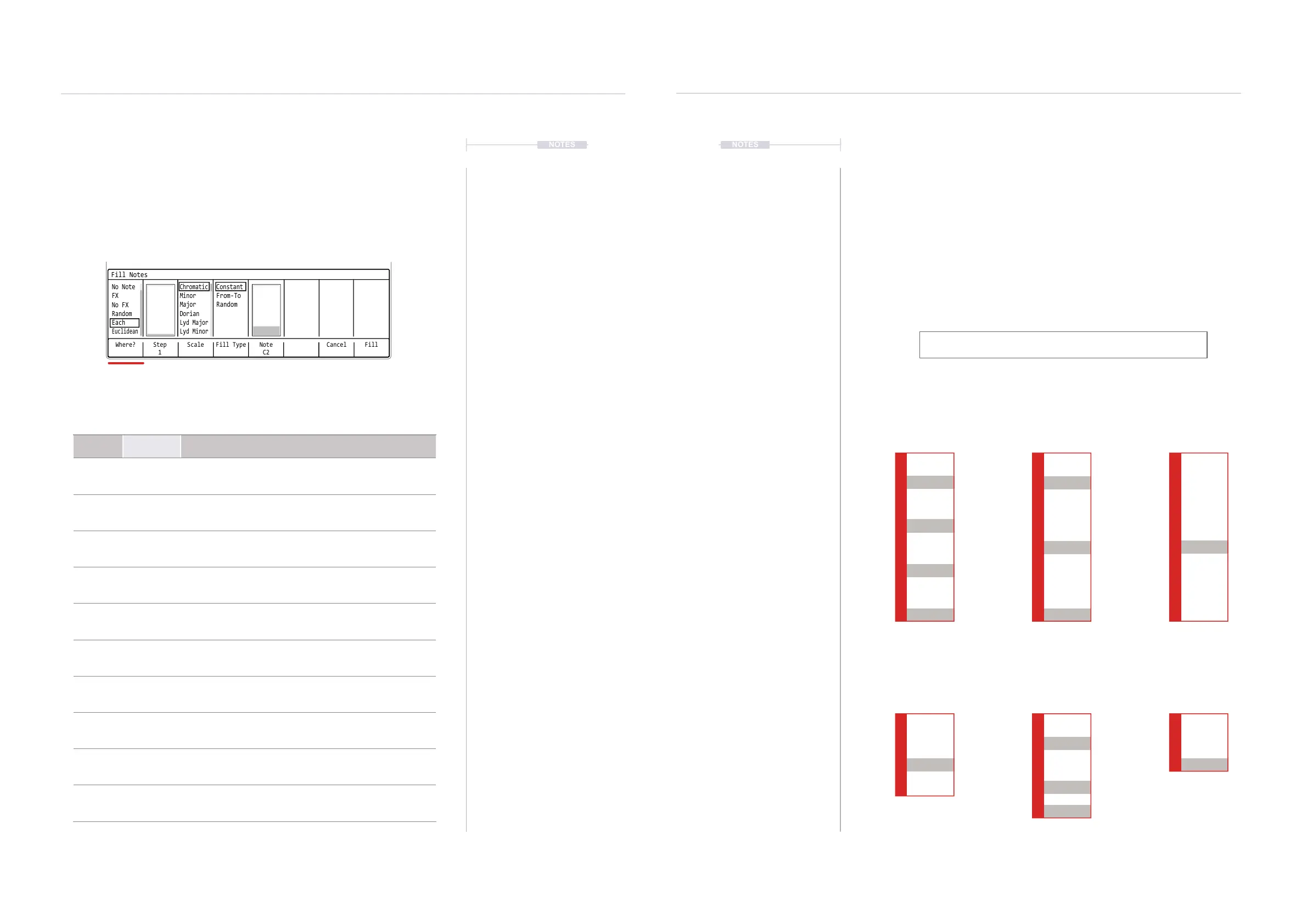
Fill Utility Generic Page Parameter - Where.
The Fill utility will present options respective to the selected step parameter.
If for example an FX parameter is selected in a range, then the ll utility will
represent FX Fills. Some elements like ‘Where?’ and ‘Fill Type’ are generic.
The ‘Where?’ option determines where in the selected step range the ll steps and dened
parameters will be placed. This will ll new steps into the steps in the range which are
empty, already lled or both depending on the selected option.
Where?
Where? Step
1
Scale Fill Type CancelNote
C2
Fill
Fill Notes
Euclidean
Chromatic
Constant
No Note
Minor
From-To
FX
Major
Random
No FX
Dorian
Random
Lyd Major
Each
Lyd Minor
Option
Sub -
Option
Description
Note -
Will populate only steps in the selected range where a
note already exists, overwriting the original value.
No Note -
Will populate only steps in the selected range where no
note exists, ie blank note steps
FX -
Will populate only steps in the selected range where an
FX parameter already exists, overwriting the original
value.
No FX -
Will populate only steps in the selected range where no
FX parameter exists, ie blank FX steps
Random -
Will populate steps in the selected range randomly for
both existing and blank steps. Density is a related option.
Random Density
Density parameter controls, in percentage how much of
the range is lled when the ‘Random’ option is selected.
Each -
Populates steps in the range with a dened step interval
which ranges from 1-32. Step is a related option.
Each Step
Step parameter controls the intervals of evenly
distributed step lls when the ‘Each’ option is selected
Euclidean -
Generates rhythmic patterns within the range based on
the population of 1-32 events. Event is a related option.
Euclidean Event
Events determine how the steps and intervals are
generated with respect to the selected step length.
Euclidean Patterns
Euclidean patterns are a more creative ll function. While the other options
perform a population based on structure, Euclidean option aims to be more
creative in generating musical sequences. Euclidean patterns are
generated based on a mathematical model where the steps and intervals
determine a pattern melody. Tracker uses ‘events’ and the step length to
calculate the steps and intervals.
Consider the following formula as rough guide for Euclidean lled patterns.
Steps will be ‘rounded’ to the nearest step location to spread as ‘evenly’ as
possible within the event and length constraints.
Examples:
Step Length / Euclidean Event Setting
8 Steps in the Length,
Event = 4.
4 Steps in the Length,
Event = 3.
8 Steps in the Length,
Event = 5.
5 Steps in the Length,
Event = 2.
8 Steps in the Length,
Event = 7.
3 Steps in the Length,
Event = 2.
Track 4
Track 4
Track 4
Track 4
Track 4
Track 4
1
1
5
3
3
7
2
2
6
4
4
5
8
---- ------- ---
---- ------- ---
---- ------- ---
---- ------- ---
---- ------- ---
---- ------- ---
---- ------- ---
---- ------- ---
---- ------- ---
---- ------- ---
---- ------- ---
---- ------- ---
---- ------- ---
D6 03
----
V 10
D6 03
----
V 10
D6 03
----
V 10
D6 03
----
V 10
D6 03
----
V 10
D6 03
----
V 10
D6 03
----
V 10
D6 03
----
V 10
D6 03
----
V 10
D6 03
----
V 10
D6 03
----
V 10
D6 03
----
V 10
D6 03
----
V 10
D6 03
----
V 10
D6 03
----
V 10
D6 03
----
V 10
D6 03
----
V 10
D6 03
----
V 10
D6 03
----
V 10 D6 03
----
V 10 D6 03
----
V 10
D6 03
----
V 10
D6 03
----
V 10
 Loading...
Loading...