Facilities For More Complex Measurements 1250 Frequency Response Analyzer
10-4 CHFR/1250/1
10.1.3 MULTIPLICATION FACTORS: x ωω
n
Pressing the x ω
n
soft key gives the user a choice of four multiplication factors, plus the
default state of "x unity" which is the "off" condition. The four choices are:
1. x (jω), which differentiates the value.
2. x (1/jω), which integrates the value.
3. x (jω)
2
, which double differentiates the value.
4. x (1/jω)
2
, which double integrates the value.
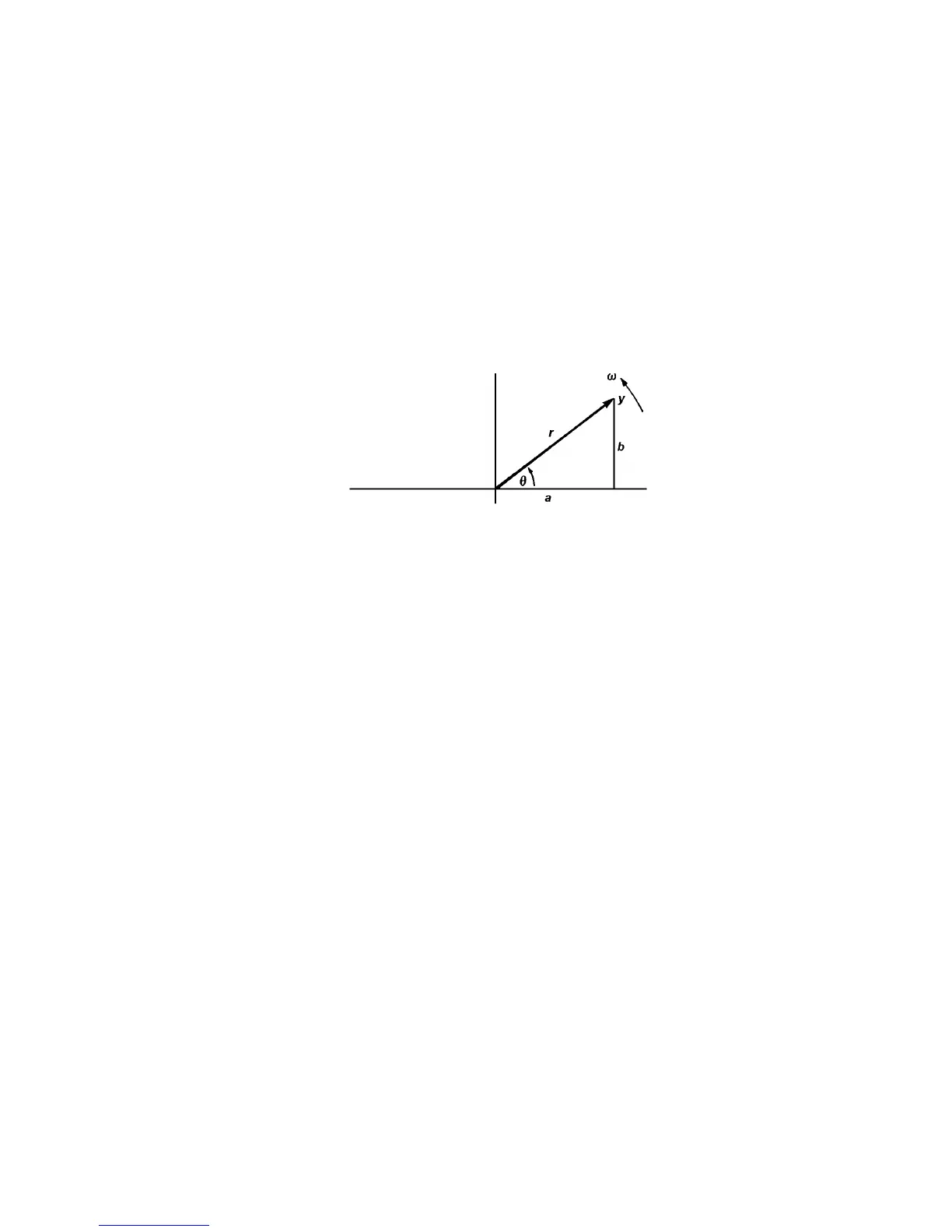
Theory. A quantity which varies sinusoidally can be represented as a vector y rotating
at a constant angular velocity ω, as shown in Fig 10.2
Figure 10.2 - Representation of Vector Quantity
The peak value is indicated by the length r, and the phase angle with respect to the 0°
reference axis at any given moment, is θ. The vector can also be represented by a
complex number, in the form a + jb.
As can be seen firom Fig. 10.2:
y = a + jb = r (cos θ + j sin θ)
and, by Euler's Formula:
r (cos θ + j sin θ) = re
j
θ
For uniformly rotating vectors, the phase angle θ is a linearly varying function of time
i.e.: θ = ωt
thus y = re
j
ω
t
and dy/dt = jωre
jwt
Hence the original quantity has been differentiated by multiplying by jω.
The other three multiplying factors act in a similar fashion. Note that this method only
applies to sinusoidal functions.
Applications. Where a required parameter cannot be measured directly, it is often
possible, by using a suitable transducer, to measure a related function. One of the
multiplying factors can then be applied to the results to derive the required data. For
example, Fig. 10.3 illustrates how various mechanical parameters can be derived from
one another by using the X ω
n
factors.
 Loading...
Loading...