BONFIGLIOLI Agile - Absolute Value of Two Orthogonal Components (2 D Vector); Absolute Value of Three Orthogonal Components (3 D Vector)

VPLC / PLC 9708/10
08/10 VPLC / PLC 97
Note:
Percentages [%] have two decimals.
For example: Value 12345
IN
= 123.45% = 1.2345
5.3.6 [341] Absolute value of two orthogonal components (2 D
vector)
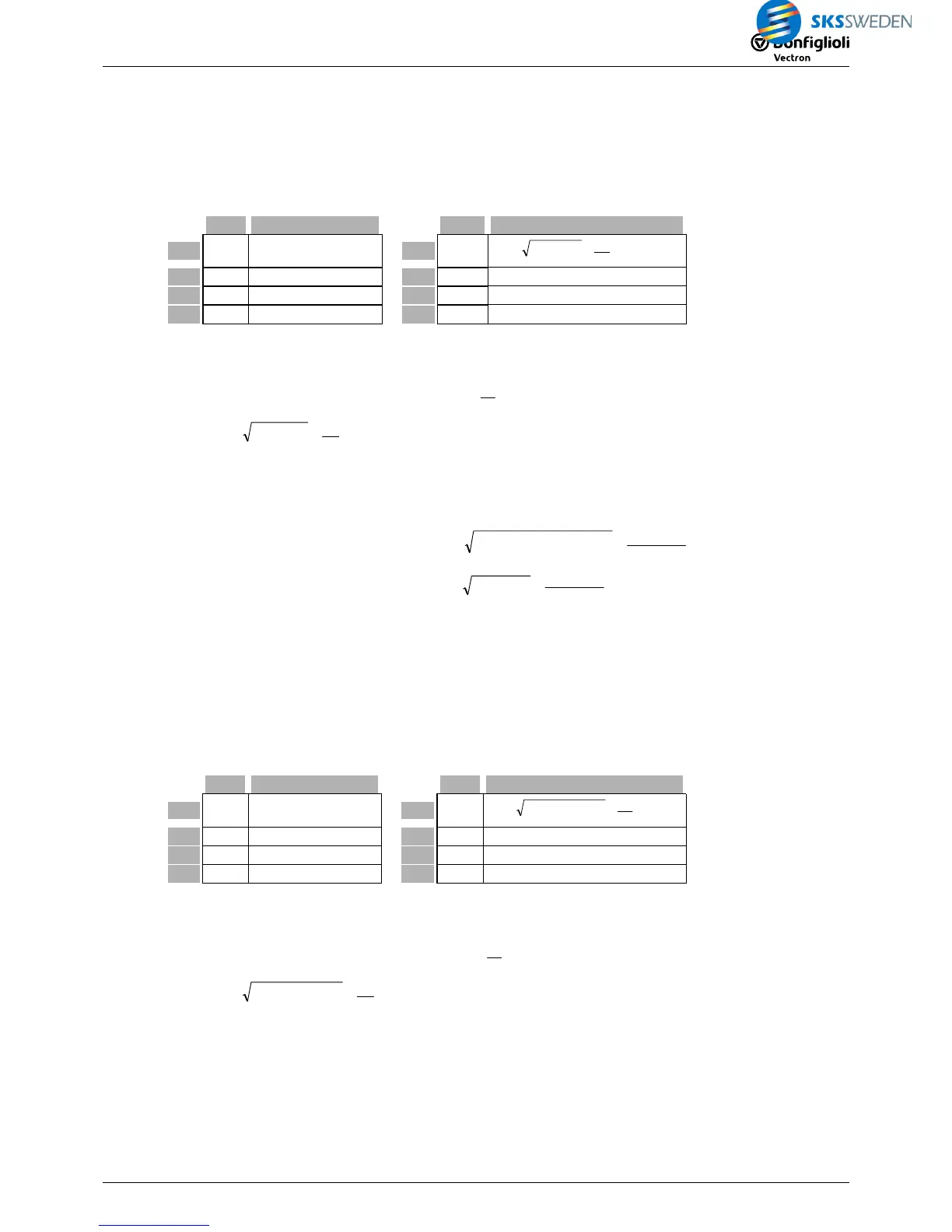
Type Function Type Function
I1 % input value 1 O1 %
P2
P1
I2I1O1
22
× +=
I2 % input value 2 O2 % inverted output = -1
I3 - - P1 % Constant (numerator)
I4 b Master Reset P2 % Constant (denominator)
Description:
The absolute value is formed from the orthogonal (square-angle) input values at I1 and I2.
The absolute value is multiplied by the constant
P2
P1
.
P2
P1
I2I12OO1
22
× += − =
As long as status TRUE is present at I4 (Master Reset), the output value O1 is 0.
Example:
I1=14000 (=140.00%)
%2 8 , 7
100,00%
5,00%
%00,212
100,00%
5,00%
%00,04%00,401O1
22
=
×=
×+=
I2=4000 (=40.00%)
P1= 500 (= 5.00%)
P2= 10000 (= 100.00%)
Note:
Percentages [%] have two decimals.
For example: Value 12345
IN
= 123.45% = 1.2345
5.3.7 [342] Absolute value of three orthogonal components (3 D
vector)
Type Function Type Function
I1 % input value 1 O1 %
P2
P1
I3I2I1O1
222
× + +=
I2 % input value 2 O2 % inverted output = -1
I3 % input value 3 P1 % Constant (numerator)
I4 b Master Reset P2 % Constant (denominator)
Description:
The absolute value is formed from the orthogonal (square-angle) input values at I1, I2 and I3.
The absolute value is multiplied by the constants
P2
P1
.
P2
P1
I3I2I12OO1
222
× + += − =
As long as status TRUE is present at I4 (Master Reset), the output value O1 is 0.
Example: