Chapter 9
FINDING THE SLOPE OF A LINE TANGENT TO A CONTOUR CURVE We con-
tinue the previous illustration with the body-mass index function in Example 1 of Section 9.4
of Calculus Concepts. Part a of Example 1 asks for
dw
dh
at the point (67, 129) on the contour
curve corresponding to the person’s current body-mass index. The formula is
dw
dh
=
−B
B
h
w
.
An easy way to remember this formula is that whatever variable is in the numerator of
the derivative (in this case, w) is the same variable that appears as the changing variable in the
denominator of the slope formula. This is why we stored B
w
as D (for denominator) and B
h
as
N (for numerator). Don’t forget to put a minus sign in front of the numerator.
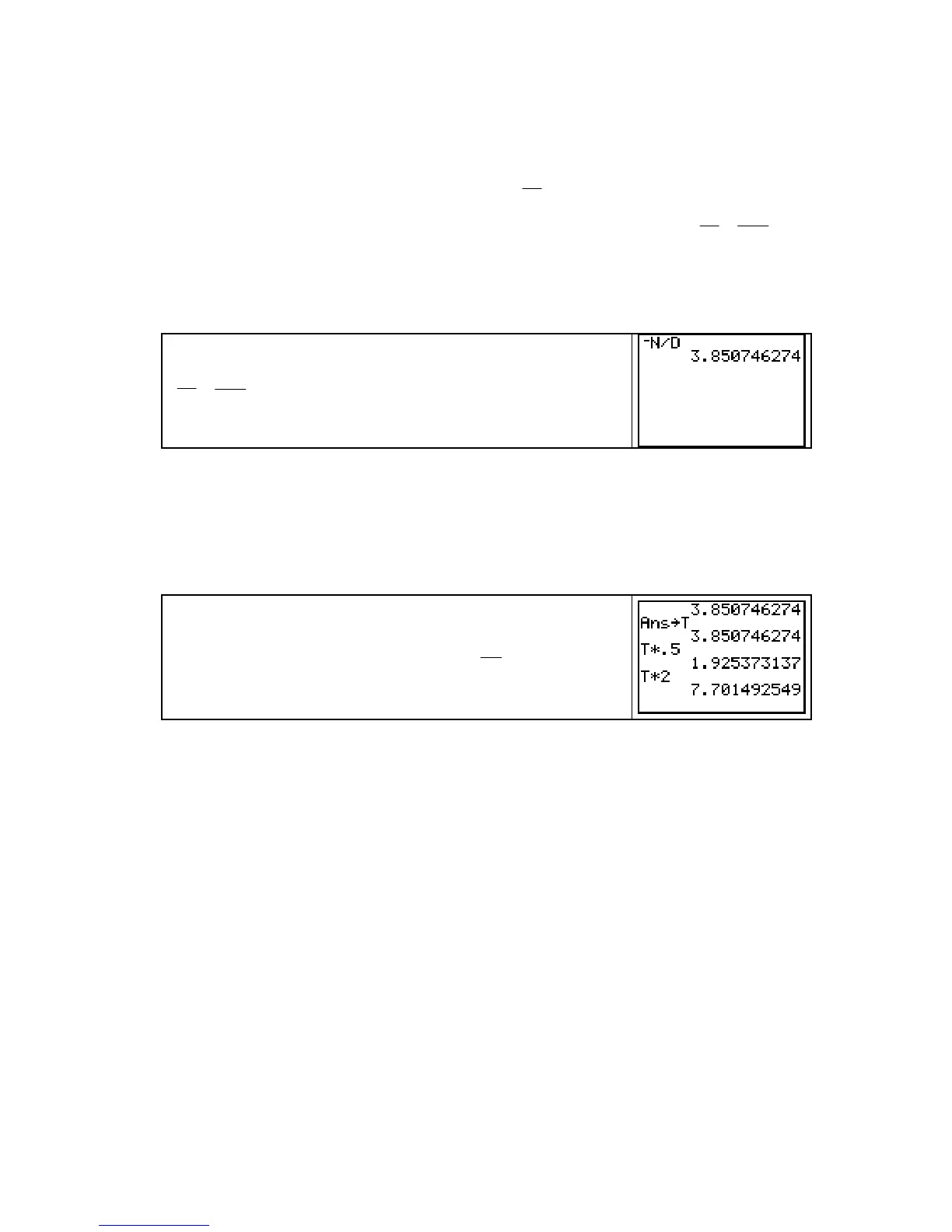
In the previous section, we stored B
h
as N and B
w
as D. So,
dw
dh
=
−B
B
h
w
=
−
N ÷ D. (Storing these values also avoids round-off
error.) The rate of change is about 3.85 pounds per inch.
COMPENSATING FOR CHANGE When one input of a two-variable multivariable func-
tion changes by a small amount, the value of the function is no longer the same as it was before
the change. The methods illustrated below show how to determine the amount by which the
other input must change so that the output of the function remains at the value it was before any
changes were made. We again continue the previous illustration with the body-mass index
function and part b of Example 1 of Section 9.4 of Calculus Concepts.
To estimate the change in weight needed to compensate for
growths of 0.5 inch, 1 inch, and 2 inches if the person’s body-
mass index is to remain constant, find ∆w ≈
dw
dh
(∆h) at the
given values of ∆h. Note that the results are changes in weight,
so the units that should be attached are pounds.
NOTE: Again, to avoid rounding error, it is easiest to store the slope of the tangent line in
some location, say
T, and use the unrounded value to calculate (as shown above).
Copyright © Houghton Mifflin Company. All rights reserved.
104
To Next Page
Loading...
Need help?
General
