Chapter 1
• There are many ways that you can enter the aligned input into L1. One method that you
may prefer is to start over from the beginning. Replace
L1 with the contents of L3 by
highlighting
L1 and pressing 2ND 3 (L3) ENTER . Once again highlight the name L1
and subtract 1900 from each number in
L1 with 2ND 1 (L1) − 1900.
On the home screen, find the linear function for the aligned data
by pressing
2ND ENTER (ENTRY) until you see the linear
regression instruction. To enter this new equation in a different
location, say
Y3, press ◄ and then press VARS ►
[Y−VARS] 1 [Function] 3 [Y3]. Press ENTER and then press
Y= to see the function pasted in the Y3 location.
• To graph this equation on a scatter plot of the aligned data, first turn off the other functions
and then return to the home screen with
2nd MODE (QUIT). Press ZOOM 9 [ZoomStat].
USING A MODEL FOR PREDICTIONS You can use one of the methods described
previously in this Guide (see pages 6 and 7) to evaluate the linear function at the indicated
input value. Remember, if you have aligned the data, the input value at which you evaluate
the function may not be the value given in the question you are asked.
CAUTION: Remember that you should always use the full model, i.e., the function you
pasted in the
Y= list, not a rounded equation, for all computations.
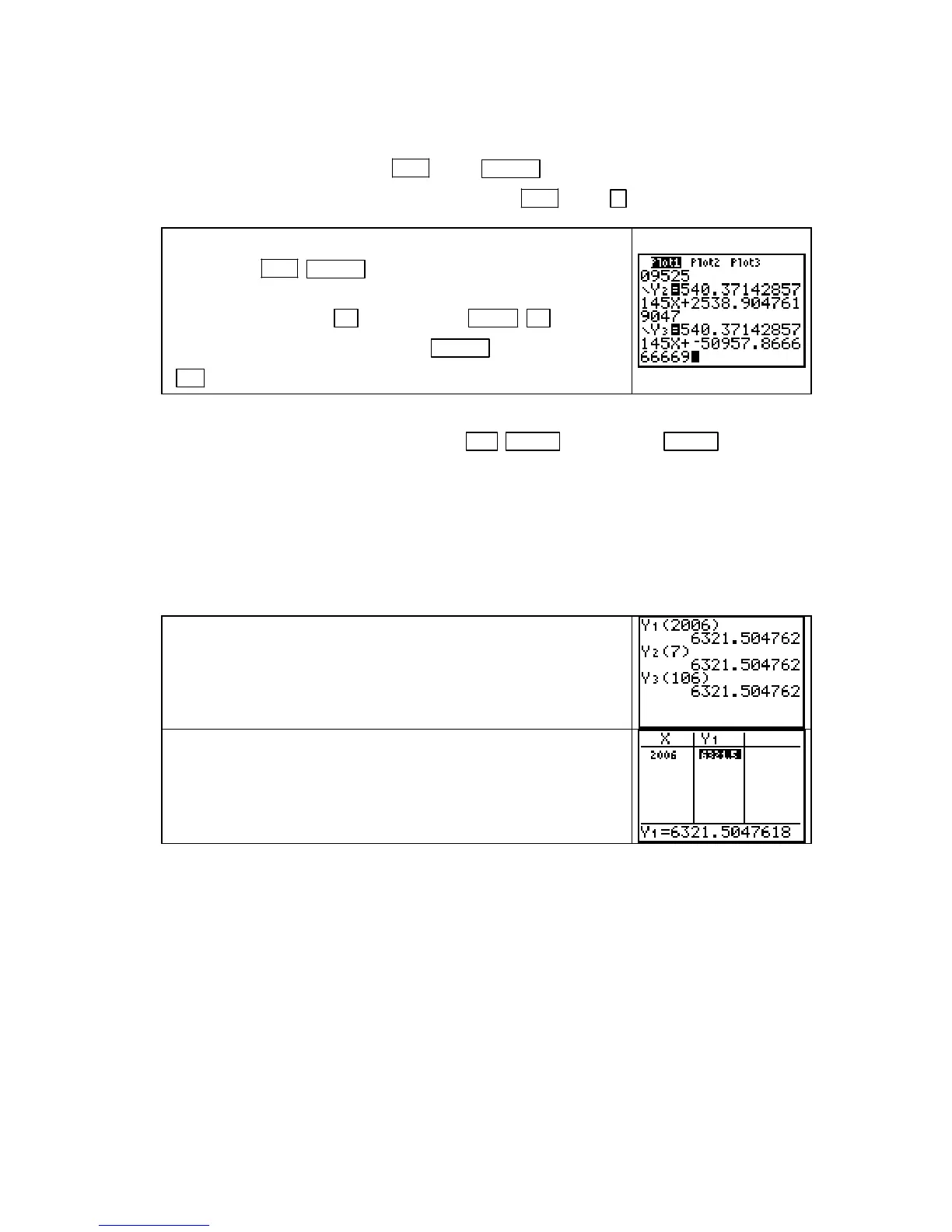
Using the function in Y1 (the input is the year), in Y2 (the input
is the number of years after 1999), or in
Y3 (the input is the
number of years after 1900), we predict that the tax owed in
2006 is approximately $6322.
You can also predict the tax in 2006 using the calculator table
(with
ASK chosen in TBLSET) and any of the 3 models found in
the previous section of this Guide. As seen to the right, the
predicted tax is approximately $6322.
NAMING AND STORING DATA You can name data (either input, output, or both) and
store it in the calculator memory for later recall. You may or may not want to use this feature.
It will be helpful if you plan to use a large data set several times and do not want to reenter the
data each time.
To illustrate the procedure, let’s name and store the modified tax output data from Section
1.2, page 32 of Calculus Concepts.
Copyright © Houghton Mifflin Company. All rights reserved.
24

 Loading...
Loading...

















