TI-83, TI-83 Plus, TI-84 Plus Guide
of the data and it should be obvious from the shape of the scatter plot the function to fit to the
data.
For instance, return to Example 1, part
b, in which we are told
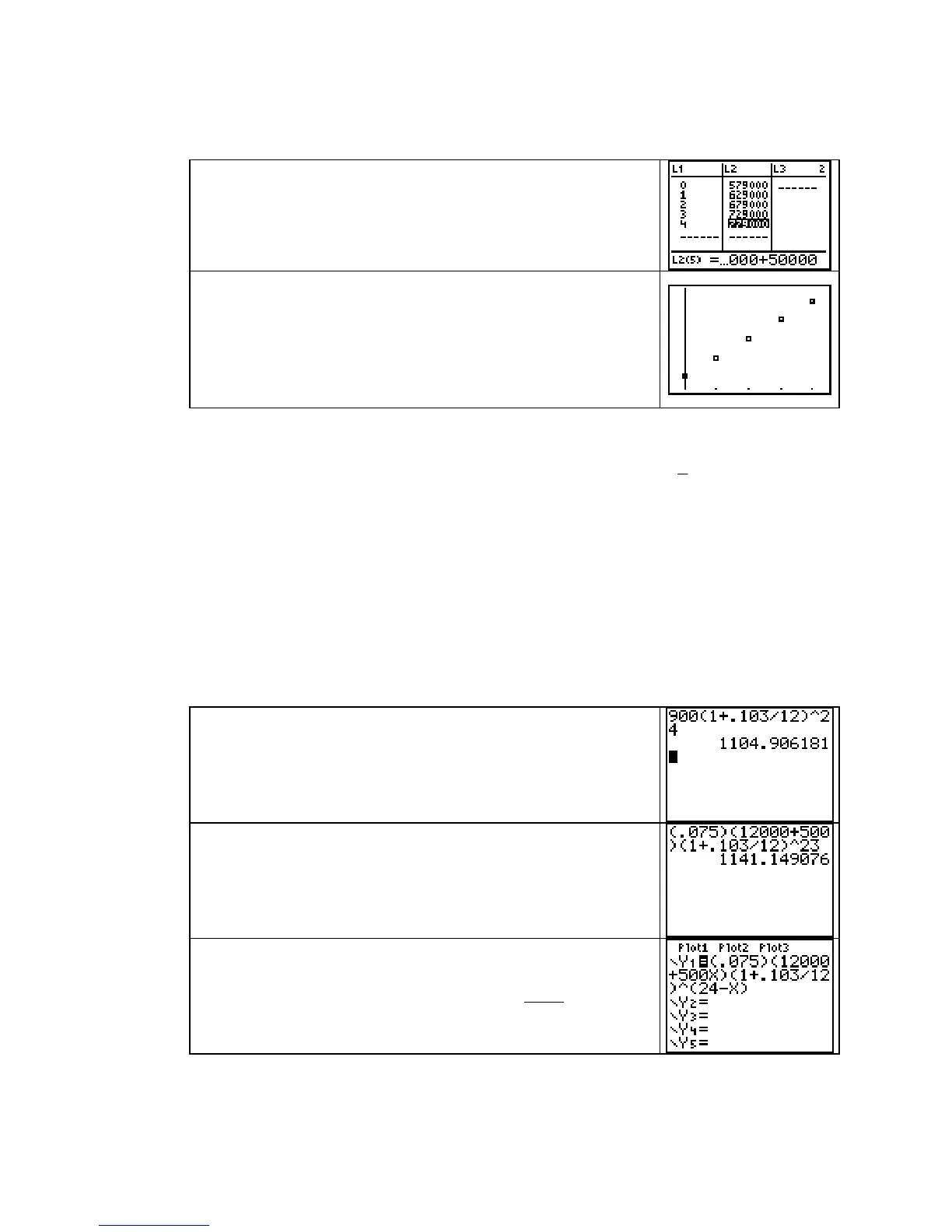
that the business’s profit grows by $50,000 each year. Note that
we assume throughout this section that initial investments are
made at time
t = 0. Simply add $50,000 to each of the previous
year’s profit to obtain about five data points.
Draw a scatter plot, and observe that the points fall in a line!
Note that if you run program
DIFF, the first differences are
constant at 50,000.
Next, find a linear equation for the data and find that the flow
rate function is
R(t) = 0.10(50,000t + 579,000) dollars per year
t years after the first year of business.
FUTURE VALUE OF A DISCRETE INCOME STREAM The future value of a discrete
income stream is found by adding, as
d increases, the terms of Rd
r
n
Dd
()1+
−
ej
where R(d) is
the value per period of the
dth deposit, 100r% is the annual percentage rate at which interest is
earned when the interest is compounded once in each deposit period,
n is the number of times
interest is compounded (and deposits are made) during the year, and
D is the total number of
deposit periods. It is assumed that initial deposits are made at time
t = 0 unless it is otherwise
stated. We use the situation on page 390 in Section 6.2 of
Calculus Concepts:
A small business begins investing 7.5% of its monthly profit into an account that pays
10.3% annual interest compounded monthly. When the company begins investing, the
monthly profit is $12,000 and is growing by $500 each month. We wish to determine
the 2-year future value of the company’s investment (assuming that profit continues to
grow in the manner described).
The first deposit is (0.075)($12,000) = $900. This deposit earns
interest for 24 months or
. $1104.91≈
The second deposit is (0.75)($12,000 + $500
1) = $937.50.
This deposit earns money for 23 months or
$1141.15
.
There is a pattern in the future values of the successive monthly
deposits:
()( )
()
24
0.103
( ) 0.075 12,000 500 1
12
d
Fd d
⎛⎞
=++
⎜⎟
⎝⎠
.
We enter the formula in Y
1.
Copyright © Houghton Mifflin Company. All rights reserved.
83

 Loading...
Loading...

















